On Correlation Effect of the Van-der-Waals and Intramolecular Forces for the Nucleotide Chain - Metallic Nanoparticles - Carbon Nanotube Binding
Abstract
Background:
The tertiary system of nucleotide chain (NC) - gold nanoparticles (NPs) - carbon nanotube (CNT) represents a great interest in the modern research and application of the bio-nano-technologies. The application aspects include, for example, the development of electronic mobile diagnostic facilities, nanorobotic design for a drug delivery inside living cell, and so on. The small NC chain represents an important stage in the understanding of the interaction mechanism of a full DNA or RNA molecule with NP and CNT. In this regard, one has to mention the development of the DNA-CNT devices for the purposes of diagnostic applications in the chemical or drug delivery.
Methods:
For the NC-NP-CNT system, we have built up a series of the molecular dynamics (MD) models with different NC-NP configurations and performed their MD analysis. The entire system (the NC chain, gold NPs and CNT) was allowed to interact with each other by the only VdW forces. The Lennard-Jones short-ranged interaction was assumed between the NC, NP and CNT. For the CNT a many body Tersoff potential having a quantum-chemistry nature was used. So far, the so-called hybrid MD approach was realized, where the quantum-chemistry potential in combination with a classical trajectory calculation applied .
Results:
The peculiarities of the NC-NP interaction and bond formation inside of a CNT matrix were investigated along with the structural and dynamical behavior. The correlation effects between the weak Van der Waals (VdW) forces and intramolecular vibrations were enlighten for the molecular system consisting of a small nucleotide chain (NC), gold nanoparticles (NPs) and carbon nanotube (CNT) using molecular dynamics (MD) simulation method.
Conclusion:
The NC intermolecular motions were estimated from MD data thereby building the distance distributions, the angular and dihedral (torsional) bond energy graphs versus simulation time at different temperatures from T=100 K up to 300 K. The MD simulation results have shown that depending on the relative NC-NP position a different scenario of bonding between the NC-NP, within CNT matrix, is possible. We have observed the possibilities of formation of weak, strong and intermediate bonds between the NP-NC, which are overestimated by a presence of CNT matrix as confined environment. The NC chain can form with a particular gold atom a close contact, while with another under the same positional and temperature conditions the weak resultant bonding formation might be possible. We estimated the fluctuations in the NP-NC bonding processes for a single gold atomic case (models 1-3, NC-1NP-CNT), for the two (model 4-6, NC-2NP-CNT) and three (model 7, NC-3NP-CNT) gold particle ones. Thus, a concurrent effect between the NC intramolecular vibrations and a weak VdW interaction between the NC and gold NP were studied in detail.
INTRODUCTION
The molecular structures like as nucleotide chain (NC) - gold nanoparticles (NPs) - carbon nanotube (CNT) are an important stage in the understanding of interaction mechanism of a whole DNA or RNA molecule with NP and CNT. A primary DNA or RNA structure consists of a linear sequence of nucleotides that are linked together by phosphodiester bonds. Nucleotides consist of 3 components: 1). Nitrogenous base - A (Adenine), G (Guanine), C (Cytosine), T (Thymine, present in DNA only) and U (Uracil, present in RNA only); 2). 5-carbon sugar which is called deoxyribose (found in DNA) and ribose (found in RNA); 3). One or more phosphate groups. From the application view, the DNA-NP-CNT system represents a great interest in many aspects of modern nano- and biotechnology, electronics and biomedical industries. For example, one has to mention the design and development of the electronic mobile diagnostic facilities for the express blood analysis, the chemical or drug delivery inside living cell, and so on, where the NC-NP-CNT system are in use. The CNTs as drug delivery vehicles have shown a potential interest due to targeting of specific cancer cells with a lower dosage rather than conventional drugs have. With regard to the different aspects of the DNA-CNT application in the DNA nanotechnology there have been great discussions from the point of view of molecular recognition processes, as a candidate material in cell drug delivery, as nucleic acid selection method (DNA aptamer) in SELEX (Systematic Evolution of Ligands by Exponential enrichment), so on. The conformational transition of aptamers (single chain DNA or RNA molecules that possess specific spatial structure) around CNT may cause some modification of the charge distribution on the CNT surface. It is worth noting that CNT surface has extremely sensitive to even a small change of the electrical charge of its environment. The replacement of even a single nucleotide for the DNA or RNA structure can modify, on the other hand, the charge environment around CNT. As a result, the CNT charge conductivity will be changed as well. So far, the DNA or RNA interactions with CNT could result to an essential modification for the charge distribution and consequent charge transfer through by the CNT surface. In the physics measurement the DNA-CNT charge distribution can be estimated trivially. This simple scheme from the point of view of application and diagnostic purposes has considered being one of the promising technologies in the DNA-CNT interaction processes with target proteins (say, of blood cells in human body) [1-13].
Recent experimental and simulation studies involve the DNA interaction with highly localized proton beams or metallic NPs (such as Ag, Au, etc.), aimed on targeted cancer therapy through the injection of metal micro- or nanoparticles into the tumor tissue with consequent local microwave or laser heating. Along with DNA-NP, the DNA-CNT system also represents a great interest now-a-days in biomedicine applications due to diagnostics and treatment of oncology diseases. Cancer, in which cells grow and divide abnormally, is one of the primary diseases with regards to how it responds to CNT drug delivery. Representing a revolutionarily potential for the biochemistry and medicine the use of CNTs in drug delivery has based on the enhancing of sufficient solubility and allowing of efficient tumor targeting. These aspects prevent CNTs from being cytotoxic and altering the function of immune cells. For today, cancer therapy involves surgery, radiation therapy, and chemotherapy. The experimental and simulation studies involve the interaction of DNA with highly localized high power beams and various nanoparticles (Ag, Au, etc.). These studies are aimed on targeted cancer therapy through the injection of metal micro- or nanoparticles into the tumor tissue with consequent local microwave or laser heating. Due to their good heat conductivities of NPs (Ag, Au, and so on) the experiments reveal that the only tumor cells to destroy, remaining normal cells undamaged. Nevertheless, such kind treatment methods are usually painful and kill normal cells in addition to producing adverse side effects [1-20].
So far, the understanding of the nucleotides – nanoparticles – carbon nanotubes dynamics and binding, as an important stage of the DNA interaction mechanism with metallic nano-particles and metallic surfaces embedded by the CNT environment, represents a potential target of modern research. In this work, the molecular dynamics (MD) simulations were performed on a small nucleotide chain (one purine and one pyrimidine) to investigate its interaction and binding processes with gold nanoparticles that happen within a carbon nanotube matrix. The behavior of a small NC model interacting with the NP-CNT system have to possess a lot of similarities with a full DNA or RNA molecule interacting in the NP and CNT environment.
MODELS AND SIMULATION METHOD
We have simulated a three component molecular system consisting of a two nucleotide chain (NC), gold nanoparticles (NPs) and a carbon nanotube (CNT) under different temperature conditions (T=100, 200 and 300 K). Two nucleotides (one pyrimidine and one purine) as in the primary structure of DNA were relaxed in the vicinity of gold particles. The nucleotide chain was located from gold atoms at distances [5-10] Å, i.e. within a range of Van der Waals (VdW) forces Fig. (1).
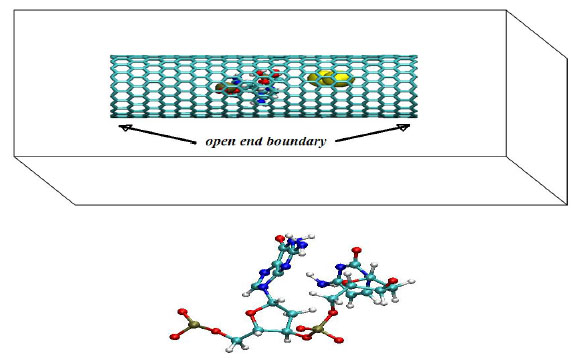
(top) A schematic view of the simulation system consisting of a two nucleotide chain (NC), gold nanoparticles (NPs) and a carbon nanotube (CNT). (bottom) A two nucleotides chain, consisting of one pyrimidine (C, cytosine) and one purine (G, guanine) as in the primary structure of DNA is shown. A primary DNA or RNA structure consists of a linear sequence of nucleotides that are linked together by phosphodiester bonds. Nucleotides consist of 3 components: (1)Nitrogenous base - A (Adenine), G (Guanine), C(Cytosine), T (Thymine, present in DNA only) and U (Uracil, present in RNA only); (2) 5-carbon sugar which is called deoxyribose (found in DNA) and ribose (found in RNA); (3) One or more phosphate groups.
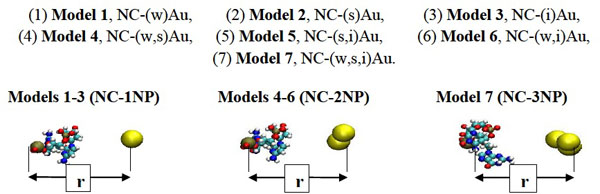
The models of the nucleotide chain (NC) interacting with 1, 2 and 3 gold nanoparticles (NPs). The positions of one of two phosphorus (P) atoms of the NC and gold NPs are shown respectively by the dark brown and yellow spheres.
During the MD simulations, first, we have generated three positional slightly different gold particles enable to interact with the NC as NC-(w)Au, NC-(s)Au and NC-(i)Au. Here the indexes (w), (s) and (i) imply the formation of preferably weak, strong and intermediate bonds between the NC-NPs, respectively. Next, we considered the different possible combinations of a two gold particle and a nucleotide chain as NC-(w,s)Au, NC-(s,i)Au and NC-(w,i)Au. Finally, we make a small triple gold cluster and simulated the NC-NPs system as NC-(w,s,i)Au. It should be noted that all the particles have the same VdW parameter values, nevertheless, depending on the initial stage of the dynamical exchange the gold nanoparticles and nucleotide chain could form arbitrary bond. Thus, we have simulated multiple NC-NP models to be able to generate various two particle (w,s), (s,i), (w,i) or three particle (w,s,i) combinations to estimate how the NC intramolecular vibrations begun to dominate over the weak non-bonding VdW attractions between the NC-NP. So far, we have investigated for the NC-NPs-CNT system seven model configurations in total under the same simulation and temperature conditions (Fig. 2).
A classical molecular dynamics study was performed using the DL_POLY_2.20 [13-15] general-purpose code. The NVT ensemble with a Berendsen thermostat and a Verlet leapfrog scheme were employed. The integration time step of the dynamical equations of motion was 1 fs. Thermostat relaxation time was between [0.1-1.5] ps, selected number of time steps more than 100000, which was enough for the basically small sizes that we simulated. The equilibration period varied between 1000-10000 steps, with a temperature scaling interval each 10 step. The entire system (the nucleotide chain, gold atoms and carbon nanotube) was allowed to interact with each other via the VdW potential only. For describing VdW interactions we used Lennard-Jones (LJ or 12-6) potential, which is commonly in use for the simulation of liquids and condensed phases. The LJ and 12-6 potential look like:
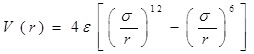 ,
,
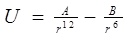
where ε, σ are the LJ interaction parameters and the cross-section interaction parameters were defined using the Lorentz-Berthelot mixing rule:
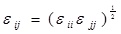 and
and
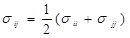 .
.
For the LJ interaction parameters we have used the data from the literature as reported, for example: ε (Au-Au)=0.039 kcal/mol, σ(Au-Au)=2.9 Å by Q. Pu et al. [16]; ε(C-Au)=0.29256 kcal/mol, σ(C-Au)=2.99 Å by Song Hai Yang and Zha Xin Wei [17]; ε(C-C)=0.1055 kcal/mol, σ(C-Au)=3.851 Å, ε(O-O)=0.156 kcal/mol, σ(O-O)=3.166 Å, by J.H. Walther et al. [18]; ε(N-N)=0.072 kcal/mol, σ(C-Au)=3.31 Å by P. Kowalczyk [19]; ε(P-P)=0.40 kcal/mol, σ(P-P)=3.33 Å by P. Ballone, R.O. Jones [20], so on. Some potentials and parameters are also shown in Appendix (Tables 1, 2), where C, O, N and P stands for carbon, oxygen, nitrogen and phosphorus atoms of the nucleotides and DNA and CC denotes the carbon atom of CNT. The force field parameters for the NC (nucleotide chain) and CNT (carbon nanotube) molecules were chosen from the DL_FIELD database [14]. The intramolecular interactions for the NC chain were described using the LJ, combined with angular and dihedral bonding potentials. The LJ, cross-interaction and bond parameters for the NC-NP-CNT system were the same as in our paper [13].
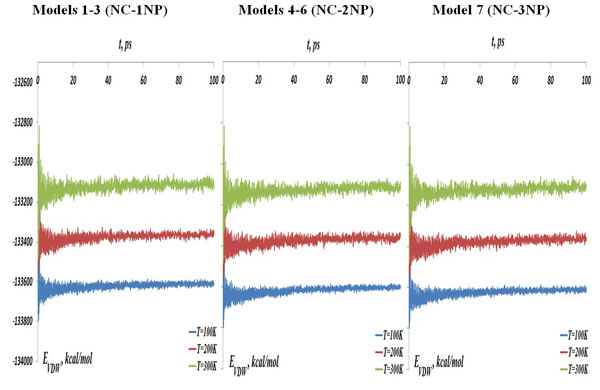
The NC-NP-CNT total potential energy, (left) models 1-3: NC-1NP, (middle) models 4-6: NC-2NP, and (right) model 7: NC-3NP, at the temperatures T=100, 200 and 300K.
For the describing CNT we have employed the quantum chemistry Tersoff potential, so far a co-called hybrid approach (the combination of quantum chemistry potential and classical trajectory calculations) has been realized to investigate the NC interaction with with CNT. In CNTs we have chemical bonding is hybridization sp2 (as graphite), which is stronger than sp3 bond (of diamond). The nature of chemical bonding in CNTs is described by quantum chemistry, through the process of orbital hybridization. The Tersoff potential in hybrid MD simulations correctly describes the nature of covalent bonding in carbon nanotube; it allows the breaking and formation of chemical bonds, that it is associated with hybridization process. Tersoff potential is pair wise potential, but coefficient in attractive term depends on local environment, thus, Tersoff potential possesses a many body nature (see, [12-15] and references therein).
RESULTS AND DISCUSSION
The MD simulations results for seven NC-NP-CNT models are shown below where the interaction distance and energy curves are coloured as: (blue) T=100 K, (red) T=200 K and (tan) T=300 K. In Fig. (3) the NC-NP-CNT total potential energy is shown for the models 1-3: NC-1NP (left), models 4-6: NC-2NP (middle) and model 7: NC-3NP (right), respectively. The curves of Fig. (3) demonstrate the increase of the interaction potential energies with the temperature. At the same time, comparing the energy data between seven models, one can also observe that the energy curves for the model 7 (NC-3NP) are located a little below than that of the models 4-6 (NC-2NP), for the models 4-6 – below than that of the models 1-3 (NC-1NP). By other words, adding each time one more gold atom to the system has slightly modifies the total potential energy of the system. Thus, a tendency of the potential energy change for a larger gold clusters is obvious.
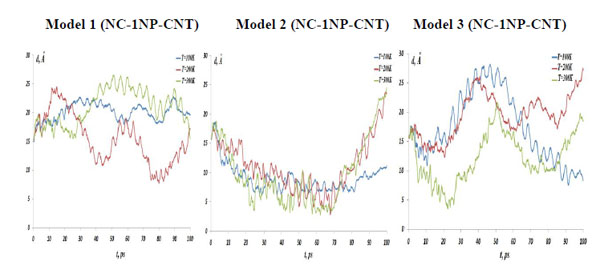
The NC-1NP-CNT distances, (left) model 1: NC-(w)Au, (middle) model 2: NC-(s)Au, and (right) model 3: NC-(i)Au, at the temperatures T=100, 200 and 300K.
Models 1-3 (NC-1NP-CNT)
In Fig. (4) the NC-NP distances depending on the temperature change are presented for the models 1-3. It should be stressed out that the NC-NP distance, as shown in Fig. (2), represents a larger distance between the NC phosphorus (P) and gold (Au) atoms. (All other NC-NP interatomic distances could be smaller than r[NC(P)-P(Au)]). Comparing the NC-NP distance distributions between three one gold particle models, we can observe that there is a different scenario of the NC-NP binding. One gold atom depending on its initial position or NC-NP orientation can form with nucleotides a weak (model 1), a strong (model 2) or an intermediate (model 3) bond. Of course, at high temperatures around T=300 K there is a NC-NP bond disruption, as the NC intramolecular vibrations begun to dominate over the weak non-bonding VdW attractions of NC-NP. Snapshots in Fig. (5) demonstrate the NC-NP positional changes inside a CNT matrix with the simulation time (T=100K). To estimate the NC intramolecular oscillations, in Fig. (6) and Fig. (7) one present the NC angular and torsion (dihedral) bond energies vs time for the temperatures T=100, 200 and 300 K. The curves of angular and torsion energies for NC-(s)Au (model 2), especially at low temperatures, slightly differ that that of the NC-(w)Au (model 1) and NC-(i)Au (model 3) ones. Also at the initial stages of the NC-1NP interactions the changes in the NC-(s)Au angular and torsion bond energies differ comparing with the NC-(w)Au and NC-(i)Au models. Thus, probably at the early stages of the interaction dynamics the nature of the NC-1NP exchange has seen to be a triggering point for the final NC-1NP bonding state.
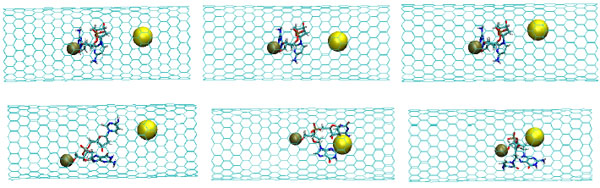
The snapshots of the NC-1NP-CNT interaction at the initial (top) and final (bottom) states (T=100K); (left) model 1: NC-(w)Au, (middle) model 2: NC-(s)Au, and (right) model 3: NC-(i)Au.
Models 4-6 (NC-2NP-CNT)
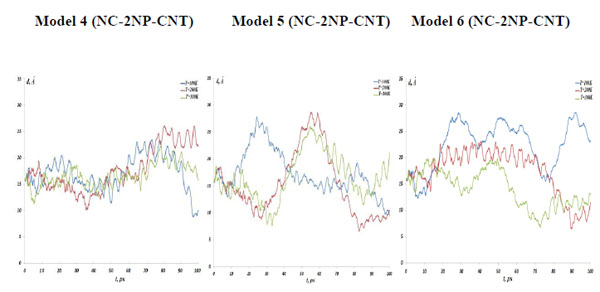
As described above, the NC interaction with gold NP inside a CNT matrix can produce preferably the weak, strong and intermediate NC-1NP bonds denoted as NC-(w)Au, NC-(s)Au and NC-(i)Au, respectively. Next, we simulated three different combinations of two gold atoms and a nucleotide chain as NC-(w,s)Au, NC-(s,i)Au and NC-(w,i)Au. In Fig. (8) the NC-2NP-CNT distances are shown for model 4: NC-(w,s)Au, model 5: NC-(s,i)Au and model 6: NC-(w,i)Au at the temperatures T=100, 200 and 300 K. Fig. (9) demonstrate the snapshots of the NC-2NP-CNT positional changes for the models 4, 5 and 6 (T=100K). From Fig. (8) and Fig. (9) one can conclude that formation of a strong bond between the NC-(w,s)Au and NC-(s,i)Au seem to be preferable, at least at low temperatures. The calculation results for the NC angular and torsion (dihedral) bond energies are presented in Fig. (10) and Fig. (11), respectively. From Fig. (10) and Fig. (11), in comparison with the NC-1NP models, one can see that the two gold atomic systems modify the initial triggering point, as noted above. Now the two gold interatomic VdW exchanges have appeared that make contribution to both the NC angular and torsion bond energy profiles, thereby influencing the final NC-2NP binding states.
Model 7 (NC-3NP-CNT)
The three gold particle system, as a next analyzing step, could be associated with a small atomic cluster possessing own oscillations and internal collective motion. Also one can assume existing of more intense VdW interactions of such gold (NP) cluster with the NC and CNT. In Fig. (12) (top) the interaction distances, the NC angular and dihedral bond energies are presented for the NC-(w,s,i)Au system (model 7) at the temperatures T=100, 200 and 300 K. The distance distribution diagrams in Fig. (12) show that a strong bond between NC-(w,s,i)Au is still kept till high temperatures. The comparison of the angular and torsion (dihedral) bond energy curves with NC-1NP-CNT and NC-2NP-CNT models are straightforward. Fig. (12) (bottom snapshots) demonstrate the NC-(w,s,i)Au positions demonstrate at the initial and final states (T=100 K). It can be observed that for the three gold particle system a close bond formation with NC inside a CNT is obvious.
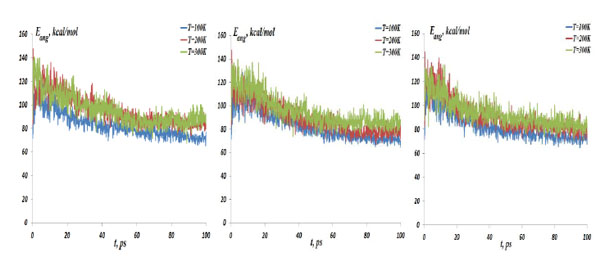
The NC angular bond energy vs time at the temperatures T=100, 200 and 300K; (left) model 1: NC-(w)Au, (middle) model 2: NC-(s) Au, (right) model 3: NC-(i)Au.
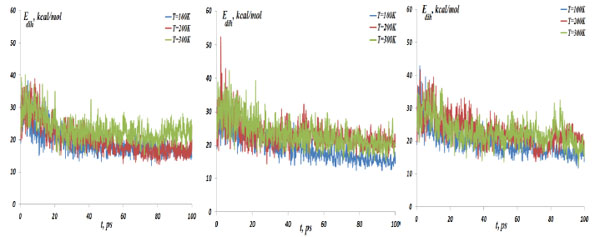
The NC dihedral bond energy vs time at the temperatures T=100, 200 and 300K; (left) model 1: NC-(w)Au, (middle) model 2: NC-(s)Au, (right) model 3: NC-(i)Au.
The NC-2NP-CNT distances, (left) model 4: NC-(w,s)Au, (middle) model 5: NC-(s,i)Au, (right) model 6: NC-(w,i)Au at the temperatures T=100, 200 and 300K.
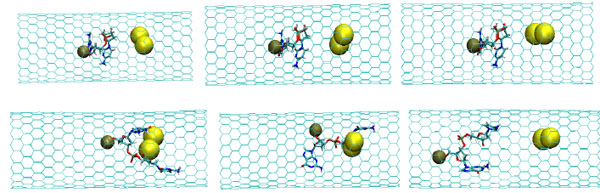
The snapshots of the NC-2NP-CNT interaction at the initial (top) and final (bottom) states (T=100K); (left) model 4: NC-(w,s)Au, (middle) model 5: NC-(s,i)Au, and (right) model 6: NC-(w,i)Au.
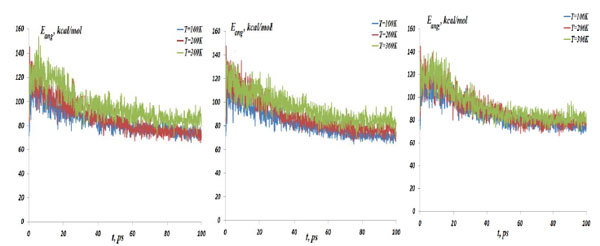
The NC angular bond energy vs time at the temperatures T=100, 200 and 300K; (left) model 4: NC-(w,s)Au, (middle) model 5: NC-(s,i)Au, (right) model 6: NC-(w,i)Au.
CONCLUSION
We have carried out a series of the MD simulations with several different models of the small nucleotide chain (NC) – gold nanoparticles (NP) – carbon nanotube (CNT) to investigate the peculiarities of VdW interactions, nature of the NC-NP bonding along with the dynamical behaviour. The MD simulation results have shown that depending on the relative NC-NP position a different scenario of bonding between the NC-NP system within a CNT matrix is possible. We have observed the possibilities of formation of weak, strong and intermediate bonds between the NP-NC, which are overestimated by the presence of CNT matrix as confined environment. The NC chain can form with a particular gold atom a close contact, while with another under the same positional and temperature conditions the weak resultant bonding formation might be possible. At high temperatures, as the NC intramolecular oscillations have grown, the picture of the NC-NPs bonding inside a CNT matrix has essentially been modified. We observe more fluctuations in the NP-NC bonding processes, not only for a single gold atomic case (models 1-3, NC-1NP-CNT) but also for the two (model 4-6, NC-2NP-CNT) and three (model 7, NC-3NP-CNT) gold particle ones. Thus, we observe a concurrent effect between the NC intramolecular vibrations and a weak VdW interaction between the NC and gold NP. In conclusion, the small NC-NP-CNT system simulated in this study represents an important stage in the understanding of the interaction mechanism of a full DNA or RNA molecule with NP and CNT. The NC intermolecular motions were estimated from MD data thereby building the distance distributions, the angular and dihedral (torsional) bond energy graphs versus simulation time at different temperatures from T=100 K up to 300 K. In conclusion, the DNA-NP-CNT system represents a great interest in many aspects of modern biochemical and nanotechnological research. In this regard, one has to mention the development of the DNA-CNT mobile electronic devices for the purposes of diagnostic applications, for the chemical or drug delivery inside the living cells and related nanorobotic design.
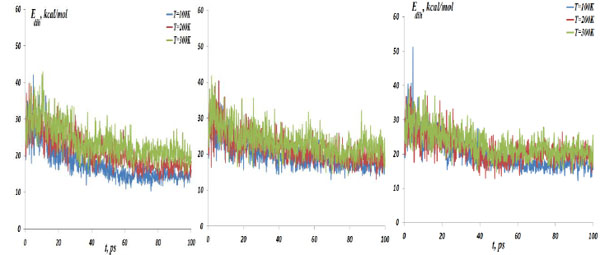
The NC dihedral bond energy vs time at the temperatures T=100, 200 and 300K; (left) model 4: NC-(w,s)Au, (middle) model 5: NC-(s,i)Au, (right) model 6: NC-(w,i)Au.
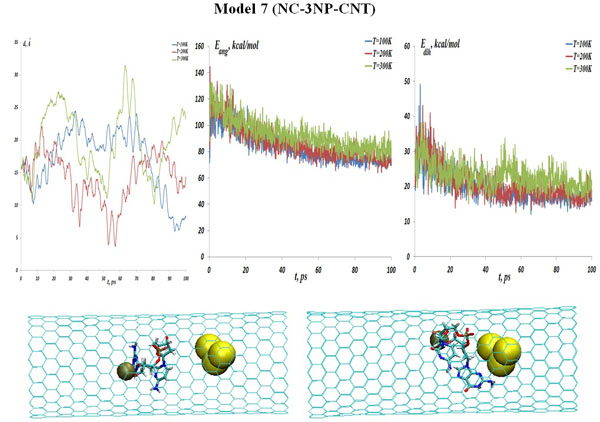
(top: from left to right) The NC-(w,s,i)Au (model 7) distances, the NC angular and dihedral bond energies at the temperatures T=100, 200 and 300K. (bottom: from left to right) Snapshots of the NC-(w,s,i) Au interaction process inside a CNT matrix at the initial and final states (T=100K).
Appendix
The 12-6 potential parameters of the NC chain.
| Pair | A,Å12 kcal/mol | B,Å6 kcal/mol | Pair | A,Å12 kcal/mol | B,Å6 kcal/mol |
|---|---|---|---|---|---|
|
C-C C-P C-O C-N O-O |
1171340 3145970 535958 730530 232116 |
667.5 1481.6 452.2 500.7 198.1 |
P-P P-O P-N N-N N-O |
8350780 1476420 1985180 450301 325886 |
3369.4 1016.6 1117.9 373.4 334.9 |
The intermolecular potential parameters of the NC chain.
| Harmonic bonds: U(r) = k(r – r0 )2/2 | |||||
| Bonds O – H |
k 300 |
r0 1.724 |
|||
| Valence angles: U(θ) = k(θ – θ0 )2/2 | |||||
| Bonds O-P-O P-O-C C-O-C N-C-N N-C-C N-C-H C-N-C |
k 100.33 106.70 106.70 133.33 133.33 133.33 133.33 |
θ0 93.300 104.510 104.510 120.000 120.000 120.000 120.000 |
Bonds C-N*-C C-N-H O-C-H H-C-H O-C-C H-C-C C-C-C |
k 109.00 109.00 112.50 112.50 112.50 112.50 112.50 |
θ0 106.700 106.700 109.471 109.471 109.471 109.471 109.471 |
| Dihedral angles: U(φ) = A[1+cos(mφ – δ)] | |||||
| Bonds P-O-C-H P-O-C-C C-O-C-H C-O-C-N C-O-C-C C-O-P-O C-N-C-C N-C-C-O N-C-C-N C-C-C-O C-C-C-N C-N-C-N H-C-N-C N-C-N-C N-C-C-H N-C-C-C H-C-C-H H-C-C-C |
A 0.3333 0.3333 0.3333 0.3333 0.3333 0.5000 2.5000 2.5000 2.5000 2.5000 2.5000 2.5000 11.250 11.250 5.6250 5.6250 5.6250 5.6250 |
δ 0 0 0 0 0 0 180 180 180 180 180 180 180 180 180 180 180 180 |
m 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 |
||
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]


