Activation Energy Calculations for Formamide–TiO2 and Formamide–Pt Interactions in the Presence of Water
Abstract
Formamide contains the four elements (C, H, O, and N) most required for life and it is attractive as a potential prebiotic starting material for nucleobase synthesis. In the presence of catalysts (for example, TiO2) and with moderate heating, formamide can pass surface energy barriers, yielding a complete set of nucleic bases and acyclonucleosides, and favoring both phosphorylations and transphosphorylations necessary for life. In the reaction mechanism, interaction with water seems to be an essential factor for the formamide molecule to function. In this paper, a formamide–water solution on a TiO$_2$ (anatase) surface is simulated using the molecular dynamics method, and activation energy calculations are performed for the temperature range of T = 250 K to T = 400 K. A correlation is established between the diffusion and density profiles for the formamide and water molecules on an anatase surface. Also, the calculated activation energies of the formamide–water–anatase and formamide–water–platinum systems are compared. A comparative analysis is performed of the behavior of formamide–water and ethanol–water interaction on the same (anatase and platinum) surfaces.
1. INTRODUCTION
The photoreaction and adsorption properties on surfaces, thermal decomposition, chemical tranformation, and other properties of the formamide molecule are widely used to understand the origins of the formation of biological molecules (nucleosides, amino acids, DNA, monolayers, etc.) needed for life. In this respect, the titanium oxide (TiO2) surface can act both as a template on which the accumulation of adsorbed molecules like formamide occurs through the concentration effect, and as a catalytic material that lowers the activation energy needed for the formation of intermediate products [1-5].
An important type of nucleoside base synthesis can be supposed to take place under UV light in the formamide reaction with a TiO2 surface, which would underlie the crucial biological significance of this mineral in making compounds of life. In the dark conditions, the experimental data on formamide adsorption at 300 K over the (001) plane of TiO2 indicate some amount of unreacted formamide and water among the products (CO, H2, NH3, HCN). Thus, some concentration of water and its involvement in formamide–TiO2 interaction was experimentally shown to be an important constituent. Besides nucleoside synthesis, formamide actively influnces in situ the hybridization of nucleotide, DNA, and RNA molecules. For example, in the presence of formamide, a U nucleotide would rather bind to an A than nothing (binding to a specific probe is better than staying single-stranded), but a U nucleotide would rather bind to nothing than a G (binding to a non-specific probe is worse than binding to nothing). In this respect, DNA is normally more stable in a double-stranded structure than in a single-stranded one; so, formamide must increase the stability of single-strandedness. On the other hand, the RNA probe binds to mRNA that is already single-stranded; mRNA does not gain any stability by being hybrid unless the probe is specific and can bind properly, thus increasing stability [1-8].
Formamide (CH3NO, hereinafter also as FM), also known as methanamide, is an amide derived from formic acid. It is a clear liquid which is miscible with water and has an ammonia-like odor. When heated strongly, FM decomposes to hydrogen cyanide (HCN) and water vapor. As a constituent, FM is also used for the cryopreservation of tissues and organs. In relation to the DNA and RNA molecules, some important formamide's properties can be outlined as follows. It stabilises RNA in gel electrophoresis by deionizing RNA; in capillary electrophoresis, it is used for stabilizing single strands of denatured DNA. FM lowers the melting point of nucleic acids, so the strands separate more readily [6]. Theoretical investigations of the chemical transformations of FM, a molecule of prebiotic interest as a precursor for biomolecules, are conducted concerning the formation of small molecules including CO, NH3, H2O, HCN, HNC, H2, HNCO, and HOCN [9].
The solvent, dehydration, adsorption, and decomposition properties of formamide on various surfaces were intensively studied in recent experimental papers [1, 2, 10–13]. Some of these experimental results are summarized and descripted in [14]. In [15], it is shown for the first time that guanine, adenine, and hypoxanthine can be produced from formamide in a single model prebiotic reaction at lower temperatures than previously reported if FM is subjected to UV irradiation during heating; this observation relaxes the requirements for prebiotic purine nucleobase formation.
Apart from experimental research, recent theoretical and simulation studies were mostly focused on the formamide–water reaction process. Several modern theoretical and molecular dynamics (MD) studies of formamide–water interactions should be mentioned in this respect [16, 17]. Nevertheless, to our best knowledge, little is known about the formamide–TiO2 surface interaction, and almost nothing has been reported on the formamide–water–TiO2 one. In this paper, using the MD simulation method, we aimed to make the first attempts to investigate the formamide–TiO2 surface interaction mechanism in detail on the atomic/molecular level. In the presence of water, we elucidate the structural, diffusional, and molecular concentration distribution effects. We consider water presence to be a stabilizing factor on the formamide–TiO2 surface interaction mechanism.
The aim of this work is to simulate the formamide–water interaction process on a TiO2 (anatase) surface and to estimate the possible activation energy barrier with the molecular dynamics method. Molecular modeling was performed for the temperature range of T = 250 K to T = 400 K, and the diffusion and density profiles were established for the formamide and water molecules on the anatase surface. The more important aspect of the present study is comparing the properties of formamide–water and ethanol–water solutions in similar environments. With the use of comparative analysis, the formamide–water interactions were correlated with the ethanol–water interactions on the same (anatase and platinum) surfaces. In this regard, metal surfaces are often used in the synthesis and degradation of oxygen-containing compounds, such as alcohols, where carbon–carbon (C–C) and carbon–oxygen (C–O) bond formation and breakage are the elementary steps in this type of process, and the metal surface plays the primary role in the efficiency and selectivity of these steps [18].
Platinum is the most widely known catalyst for the oxidation of molecules like ethanol. The dissociative adsorption of formamide on the Pt(111) surface at low doses can result in the formation of coadsorbed NH3 and CO at 170 K; with heating, the hydrogen-bonding interactions lead to the autocatalytic desorption of formamide at 223 K [19]. On the other hand, we should mention the ability of ethanol to recover RNA from formamide-containing solutions, formamide-sensitive and ethanol-sensitive mutations, the effects of formamide and ethanol agents on biological systems, and so on, which present a topical problem of modern research and technological applications [20–22].
2. RESULTS AND DISCUSSION
2.1. Pure Formamide/TiO2 Surface
In the Supplement section, the materials and methods regarding the simulated systems are described in detail. We first simulated the interaction process of pure formamide and a TiO2 surface. A comparative analysis has been performed of the formamide–TiO2 (anatase) and formamide–Pt (platinum) surface interactions. The specifics of the formamide concentration effect on two different surfaces provide better comparison data with regard to the formamide–surface interaction mechanism.
2.1.1. MD-simulated Snapshots and Z-density Distributions
Fig. (1) (top snapshots) show the formamide concentration distribution on the TiO2 and Pt surfaces, respectively. In the formamide–TiO2 (left) and formamide–Pt (right) interactions, both surfaces behave as an amorphous solid. Thermal vibrations slightly displace the TiO2 and Pt atoms from their mean equilibrium positions. In comparison with the Pt surface, the TiO2 (anatase) one is observed to behave more like an amorphous matter because charged particles of the TiO2 surface are subject to more intense interactions than the neutral atoms of the platinum one.

Top: snapshots of pure formamide in the presence of TiO2 (left) and Pt (right) surfaces. Bottom: Z-density distributions of pure formamide on the TiO2 (left) and Pt (right) surfaces.
Fig. (1) (bottom daigrams) also demonstrate the interfacial structure of formamide adsorption on TiO2 and Pt surfaces. The diagrams were constructed by calculating normalized formamide density profiles as functions of the distance perpendicular to the corresponding surfaces. The adsorption layers are seen in Fig. (1), where a density plot on each surface (formamide/TiO2, left; formamide/Pt, right) shows the distrubuiton of formamide molecules on the surfaces symmetrically surrounding the solution. In the formamide/Pt density profile (Fig. (1), right), there is a well-defined first adsorption layer with a thickness of 2 to 4 Å and two more diffuse layers with a thickness of 5 to 8 Å (for the left Pt wall, from –25 Å to –15 Å; for the right Pt wall, from 15 Å to 25 Å). In the formamide/TiO2 density profile (Fig. (1), left), a rather weak adsorption layer is seen between two diffuse layers at more extended distances than in the formamide/Pt one (on the left, there is a TiO2 wall from –30 Å to –15 Å; on the right, there is a TiO2 wall from 15 Å to 30 Å). For both surfaces, in the distances from the –15 Å to 15 Å, the relative formamide densities approach unity as it would be expected for a bulk environment without electrode influence. According to the present results, the interfacial region for formamide adsorption on a TiO2 surface covers the range of 2–10 Å with disorganization increasing towards the bulk liquid. The density distribution amplitudes for the formamide/TiO2 surface are twice lower than for the formamide/Pt one. Small asymmetry in the peaks of the density profile diagram shown in Fig. (1) is likely due to an annealing process we employed. We have equilibrated the whole system (the solution and adsorbing surface walls) with a temperature step of 25 K, starting from the crystal phase and heating it up to room and higher temperatures. With shorter steps (for example, 1–5 K), the relaxation procedure would yield a smoother transition to the equilibrium state, although computation time would grow rapidly.
2.1.2. Activation Energy Calculations
It is believed that the self-diffusion coefficient follows an Arrhenius-like expression with temperature [23]:
Following the Arrhenius equation, we have constructed a relation between ln D(T) and reciprocal temperature in Kelvin for the formamide/TiO2 and formamide/Pt surfaces (Fig. (2): the solid line for formamide on TiO2 and the dashed line for formamide on Pt). As seen in Fig. (2), the diffusion coefficient of formamide in the presence of TiO2 and Pt surfaces obeys the Arrhenius equation. Thus, we observe a similar behavior of the ln D(T) vs f(1/T) dependence for both TiO2 (anatase) and Pt (platinum) surfaces, with which formamide molecules interact – in spite of the different density distribution behavior as described above. The calculated apparent activation energies (E) of diffusion are respectively 2.3 and 2.1 kcal/mole for formamide/TiO2 and formamide/Pt (Table 1).
Activation Energy Results for Formamide, Ethanol, and Water in the Simulated Models
| System | Ewat, kcal/mole | Eform, kcal/mole |
|---|---|---|
| (TiO2)(CH3NO) | - | 2.3 |
| (Pt)(CH3NO) | - | 2.1 |
| Ewat, kcal/mole | Eform, kcal/mole | |
| (TiO2)(H2O)(CH3NO) | 3.0 | 2.7 |
| (Pt)(H2O)(CH3NO) | 2.1 | 2.9 |
| Ewat, kcal/mole | Eeth, kcal/mole | |
| (TiO2)(C2H5OH) | - | 1.8 |
| (Pt)(C2H5OH) | - | 1.1 |
| Ewat, kcal/mole | Eeth, kcal/mole | |
| (TiO2)(H2O)(C2H5OH) | 3.5 | 2.7 |
| (Pt)(H2O)(C2H5OH) | 3.7 | 2.9 |
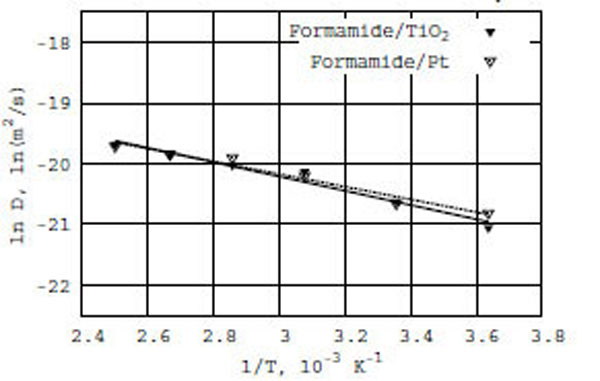
Relation between ln D(T) and reciprocal of temperature in Kelvin; solid line for formamide on TiO2 (anatase) and dashed line for formamide on Pt (platinum) surfaces.
2.2. Formamide–Water/TiO2 Surface
Next, we simulated formamide interaction with a TiO2 surface in the presence of a water solvent. Like in the previous section, we compare the formamide–surface interaction mechanism for two different material models: TiO2 (anatase) and Pt (platinum).
2.2.1. Z-Density Distribution and Activation Energy Calculations
In Fig. (3) (top snapshots), the formamide–water concentration distributions are shown for the TiO2 and Pt surfaces, respectively. In the snapshots, we can see the formation of adsorption layers near the surfaces in both systems: formamide--water/TiO2 (left) and formamide–water/Pt (right), although the density distribution on the Pt surfaces looks more dense and well-defined than on the TiO2 surfaces.
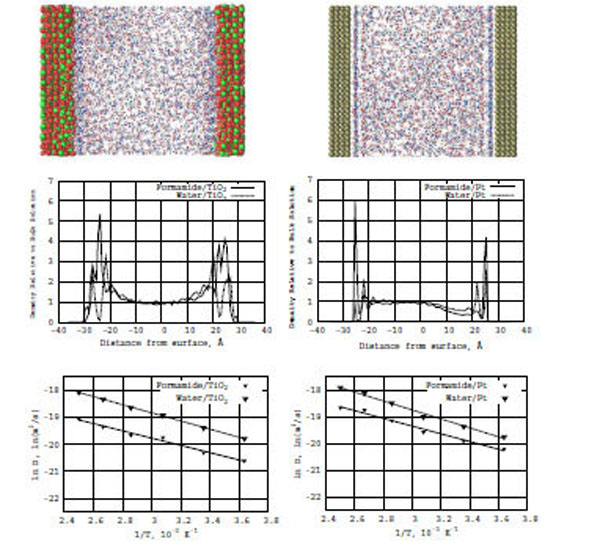
Top: Snapshots of a formamide-water mixture in the presence of TiO2 (anatase; left) and Pt (platinum; right) surfaces. Middle: Z-density distributions of formamide (the solid line) and water (the dashed line) on the TiO2 (left) and Pt (right) surfaces. Bottom: The relation between ln D(T) and reciprocal temperature in Kelvin; the solid line is for formamide and the dashed line is for water in the presence of TiO2 (left) and Pt (right) surfaces.
Also, Fig. (3) (bottom diagrams) represent the formamide–water Z-density distributions on the TiO2 (left) and Pt (right) surfaces, respectively. The inclusion of water to the formamide–TiO2 system significantly modifies the density distribution profiles normal to the surface. The amplitudes of the density distribution for the formamide/TiO2 surfaces increase and become comparable with those for the formamide/Pt one. It is clear that water strongly influences the formamide–TiO2 system as regards the mobility of formamide molecules interacting with the TiO2 surface.
From the Arrhenius equation, we have constructed a relation between ln D(T) and reciprocal temperature in Kelvin for the formamide–water/TiO2 and formamide–water/Pt surfaces. In Fig. (3), solid lines for formamide and dashed lines for water show the ln D(T) vs f(1/T) dependence for the TiO2 (left) and Pt (right) surface, respectively. From the ln D(T) graphs, we calculated the diffusion activation energies (E) for the formamide-water/TiO2 and formamide-water/Pt (Table 1) systems. The activation energies of water and formamide are Ewat = 3.0 and Eform = 2.7 kcal/mole (on TiO2), and Ewat = 2.1 and Eform = 2.9 kcal/mole (on Pt), respectively. Thus, the inclusion of water increases the diffusion ability of formamide molecules on the TiO2 (anatase) surface. In the formamide-water/TiO2 system, water has a definitely higher activation energy and lower diffusive ability than in the the formamide-water/Pt one.
2.2.2. Intermolecular Structure
Hereinafter, Hf, HW, Of, and OW denote, respectively, the hydrogen atoms of formamide and water and oxygen atoms of formamide and water.
Liquid-Liquid Ordering.
The structure of liquids is usually expressed in terms of radial distribution functions (RDF) g(r). The most structured and interesting g(r) functions for a liquid like a formamide-water solution correspond to oxygen-oxygen and oxygen-hydrogen bonding. Fig. (4) (top and bottom) show the structural arrangement peculiarities in terms of RDF graphs for the Of-Of, OW-OW, Of-HW, and OW-Hf atomic pairs in the formamide-water mixture (left: formamide-water/TiO2; right: formamide-water/Pt). It is seen that the behavior of the water oxygen atom pair (OW-OW) is more ordered than that of the formamide-formamide one (Of-Of) as the first g[OW-OW] RDF peak is located at 3.0 Å from the zero point, which is 1.0 Å shorter than the location of the g[Of-Of] RDF peak. At the same time, the Of-HW interaction is much stronger than that in the OW-Hf atomic pair. The amplitude of the first g[Of-HW] RDF peak located at 2 Å is twice higher than that of g[OW-Hf], which is located around 2.8 Å. Both TiO2 and Pt surfaces exhibit similar liquid-liquid ordering, although some small changes can be seen (Fig. (4)) in the g[Of-HW] and g[Of-Of] functions.
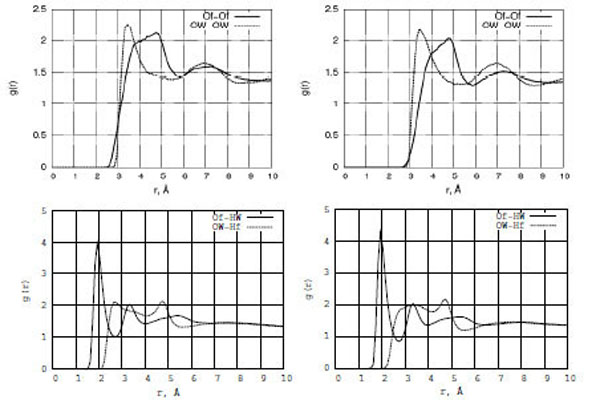
The radial distribution functions (RDF) for Of-Of, OW-OW, Of-HW, and OW-Hf of the formamide-water mixture interacting with the TiO2 (left) and Pt (right) surfaces.
Liquid-Surface Ordering.
In Fig. (5) (top and bottom), the RDF graphs illustrate formamide-water/surface interactions for TiO2 (left) and Pt (right) walls. It is seen from the left diagrams that water (both oxygen (OW) and hydrogen (HW) atoms) interacts with the TiO2 wall surfaces stronger than formamide (oxygen (Of) and hydrogen (Hf)). The first g[Ti-OW] and g[O-OW] RDF peaks are three times larger than those of g[Ti-Of] and g[O-Of], respectively, and their locations are shorter by 0.4-0.5 Å. The first g[Ti-HW] and g[O-HW] RDF peaks are also larger and located much closer to zero than those of g[Ti-Hf] and g[O-Hf], respectively. Thus, water molecules are closer to the TiO2 surface than to the formamide one. For Pt walls (the right diagrams), we do not observe any substantial difference between g[Pt-OW] and g[Pt-Of] or g[Pt-HW] and g[Pt-Hf]. Of course, the interaction between the oxygen atoms of water and formamide on a neutral Pt surface is stronger than between the hydrogen atoms of water and formamide. However, TiO2 and Pt surfaces have different nature of interaction with water and formamide solution.
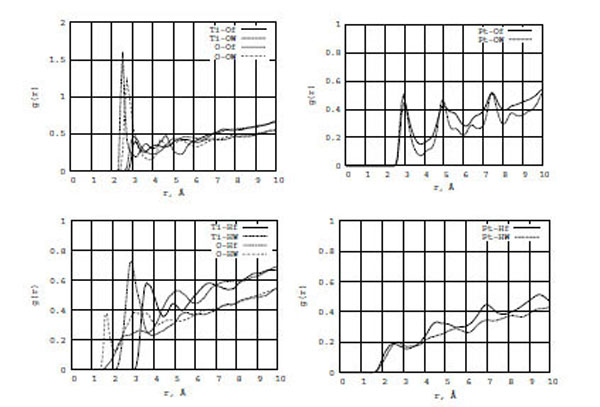
The RDF for the formamide (Of, Hf) and water (OW, HW) atoms on the TiO2 (left) and Pt (right) surfaces.
2.3. Correlation with Ethanol-Water/TiO2, Pt Surfaces
In this section, we perform a comparative analysis of formamide-water/TiO2 interaction by modeling an ethanol-water mixture on the same TiO2 (anatase) and Pt (platinum) surfaces. We study ethanol-water/(TiO2, Pt) systems under similar thermodynamic conditions and environmental geometry. In this regard, it should be noted that a lot of possible applications of ethanol have been considered in recent years, which arouses great interest in studying its chemical and physical properties. The most popular application is fuels because of a decrease in the available petroleum resources; ethanol is one of the most important renewable fuel. For ethanol to be a fuel, the water content in ethanol should be less than 1.3% [24], which is hard to reach by crystallization. An alcohol-water mixture often shows quite different properties than the corresponding pure components. Of particular interest are the structure and diffusion properties, which play important roles in the theoretical study and technological applications involving mass transfer [25]. In addition, from a microscopic viewpoint, the knowledge of solution structure behavior is very fundamental to understanding and elucidating the mixture diffusion phenomenon. For ethanol on a platinum surface, the latter is a catalyst for the activation of carbon-carbon and carbon-oxygen bond breakage, which is an elementary step in the oxidation of alcohols [18]. Water and ethanol can also find other applications than in fuels - in particular, as solvents accelerating the aging of some polymeric materials [26] and in cooling systems because of their suitable thermophysical and technological characteristics [27].
2.3.1. Z-Density Distribution and Activation Energy Calculations
First, we simulated the interaction of pure ethanol with TiO2 and Pt surfaces. Fig. (6) (top diagrams) demonstrate the Z-normalized ethanol density distributions from TiO2 and Pt surfaces, respectively. From the density profile (Fig. 6, left) we can see more extended adsorption and diffusive layers in the ethanol/TiO2 system than in the ethanol/Pt one (Fig. 6, right). In comparison with pure formamide/(TiO2, Pt) as discussed above, the Z-density distributions for pure ethanol/(TiO2, Pt) are similar, although some small changes in the peak amplitudes can be observed.
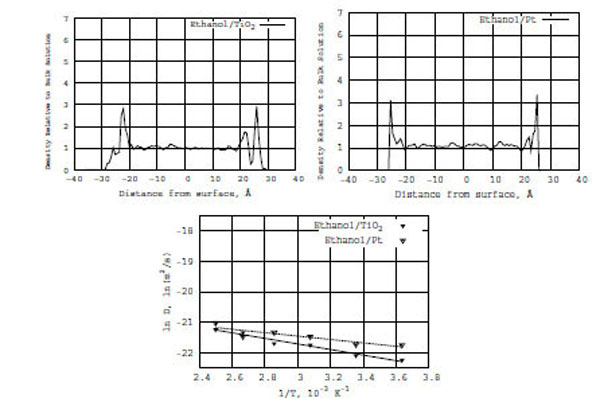
Top: Z-density distributions of pure ethanol on the TiO2 (left) and Pt (right) surfaces. Bottom: Relation between ln D(T) and reciprocal temperature in Kelvin; ethanol in the presence of TiO2 (solid line) and Pt (dashed line) surfaces.
In Fig. (6) (the bottom diagram), like for the formamide/TiO2 and formamide/Pt models, a relation is built between ln D(T) and reciprocal temperature in Kelvin (the solid line is for ethanol on TiO2 and the dashed line is for formamide on Pt). It is seen from Fig. (6) that the diffusion coefficient of pure ethanol on the TiO2 and Pt surfaces obeys the Arrhenius equation. From the ln D(T) vs f(1/T) graphs, the calculated activation energies (E) of diffusion for ethanol/TiO2 and ethanol/Pt are 1.8 and 1.1 kcal/mole, respectively (Table 1). The ethanol activation energy on the TiO2 surface is 0.5 kcal/mole lower than that of formamide/TiO2; it is twice lower on the Pt surface than that of formamide/Pt one. The comparison of activation energies for pure ethanol/(TiO2, Pt) and formamide/(TiO2, Pt) in Table 1 is straightforward.
In Fig. (7) (top snapshots), the ethanol-water concentration distributions are shown between two symmetric TiO2 (left) and Pt (right)surfaces. The pictures of the molecular densities are similar to the formamide-water ones as described above.
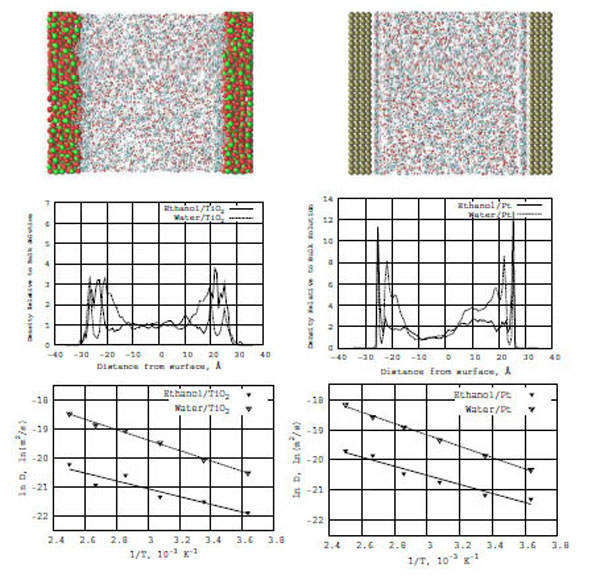
Top: Snapshots of the ethanol-water mixture in the presence of TiO2 (left) and Pt (right) surfaces. Middle: Z-density distributions of ethanol (solid line) and water (dashed line) on the TiO2 (left) and Pt (right) surfaces. Bottom: Relation between ln D(T) and reciprocal temperature in Kelvin: ethanol (solid line) and water (dashed line) in the presence of TiO2 (left) and Pt (right) surfaces.
Fig. (7) (bottom diagrams) also demonstrate the ethanol-water interfacial structure formations and adsorption on TiO2 and Pt surfaces, respectively. The diagrams show the Z-normalized densities of ethanol and water on the corresponding surfaces. In the density profile (Fig. 7, right), there are sharp first (adsorption) layers for ethanol-water/Pt in comparison with ethanol-water/ TiO2 (Fig. 7, left). The second (diffuse) water layers on both TiO2 and Pt surfaces are quite extended, which is seen when comparing the water density distribution graphs shown above for formamide-water/TiO2 and formamide-water/Pt. It is clear that water in both models (ethanol-water and formamide-water) has a substantial influence on the behavior of these two different systems. In other words, water's diffusive ability determines all the dynamics and structure formations in the models under consideration.
For the ethanol-water/TiO2 and ethanol-water/Pt models, we have built a relation between ln D(T) and reciprocal temperature in Kelvins using the Arrhenius equation. In Fig. (7), solid lines for ethanol and dashed lines for water show the ln D(T) vs f(1/T) dependence for the TiO2 (left) and Pt (right) surfaces. From the ln D(T) graphs, we have calculated the diffusion activation energies (E) for ethanol-water/TiO2 and ethanol-water/Pt (Table 1). The activation energies of water and ethanol are Ewat = 3.5 and Eeth = 2.7 kcal/mole (on TiO2) and Ewat = 3.7 and Eeth = 2.9 kcal/mole (on Pt), respectively. It is easy to see that the ethanol and formamide activation energies are very close to each other. Only the water activation energies differ (the comparison of the data in Table 1 is straightforward). Water strongly influences the diffusion capabilities of formamide and ethanol on both TiO2 and Pt surfaces. Thus, introducing a water solvent seems to be an important factor of the structural and dynamic behavior of the studied systems under investigation.
2.3.2. Intermolecular Structure
Hereinafter, He, Hf, HW, Oe, Of, and OW denote, respectively, the hydrogen atoms of ethanol, formamide, and water; and oxygen atoms of ethanol, formamide and water.
Liquid-Liquid Ordering.
The RDF g(r) for the ethanol-water mixture, were built like the formamide-water RDF in the previous section. From Fig. (8) (top graphs), ethanol-ethanol and water-water ordering, g[Oe-Oe] and g[OW-OW], looks much stronger than formamide-formamide and water-water as discussed above for g[Of-Of] and g[OW-OW] (Fig. (4)). Both RDF characteristics - the amplitudes and positions of the first peaks - substantially differ in the top graphs of Figs. (8) and (4). At the same time, formamide-water ordering is stronger than ethanol-water one (see the bottom graphs of Figs. (8) and (4) for g[Oe-HW] and g[OW-He] in comparison with g[Of-HW] and g[OW-Hf], respectively.

The RDF for Oe-Oe, OW-OW, Oe-HW, and OW-He of the ethanol-water mixture on the TiO2 (left) and Pt (right) surfaces.
Liquid-Surface Ordering.
In Fig. (9), the RDF graphs show the ethanol-water interactions with TiO2 (left) and Pt (right) surfaces. The most interesting are g[Ti,O-He] and g[Ti,O-HW] (the bottom graph). The amplitudes of the first RDF peaks of g[Ti-He] and g[O-He] are two-three times larger than those of g[Ti-HW] and g[O-HW], respectively. Since the first peaks of both RDF, g[O-He] and g[O-HW], are located very close to zero (< 2 Å), ethanol rather than water molecules would be dominant on the surface. At the same time, comparing Figs. (9) and (4) - g[Ti,O-Of], g[Ti,O-Hf], g[Ti,O-Oe], and g[Ti,O-He] - we conclude that in the formamide-water/ (TiO2, Pt) interactions water molecules would actviley push formamide molecules from the surface to the bulk areas, while in the ethanol-water/(TiO2, Pt) interactions ethanol rather than water molecules would dominate on the surface areas. Thus, including water in consideration, one can conclude that it has different influence on the formamide/(TiO2, Pt) and ethanol/(TiO2, Pt) interaction processes, which results in different structural and diffusion effects.
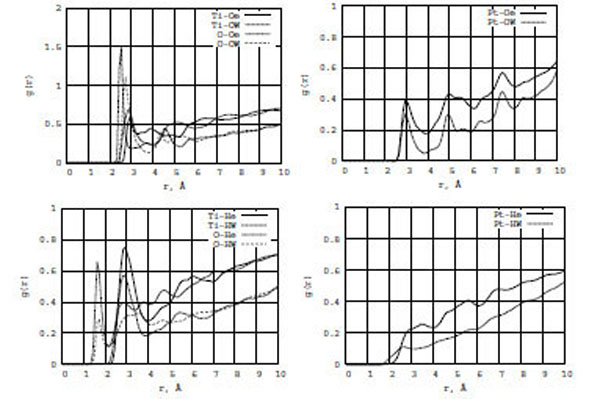
RDF for ethanol (Oe, He) and water (OW, HW) atoms on the TiO2 (left) and Pt (right) surfaces.
3. CONCLUSIONS
Based on the molecular dynamics method and using the DL_POLY_4.03 code, we simulated the formamide-water interaction process on the TiO2 (anatase) surface. The density distribution and activation energy calculations were performed for the temperature range of T = 250 K to 400 K. For pure formamide/TiO2, the activation energy of diffusion was calculated to be about 2.3 kcal/mole. The density profile of formamide/TiO2 has a weak adsorption layer between two diffuse layers. The activation energies of water and formamide on the TiO2 surface were calculated to be Ewat = 3.0 and Eform = 2.7 kcal/mole, respectively. The inclusion of water in the formamide-TiO2 model substantially changes the density distribution profiles normal to the surface; the amplitude of the density distribution for the formamide/TiO2 surface increases. A correlation was found between the diffusion and density properties of the formamide-water/TiO2 and formamide-water/Pt systems. A comparison of the water density distribution in the formamide-water/TiO2 and formamide-water/Pt systems shows that the second (diffuse) water layers on both TiO2 and Pt surfaces are quite extended. The activation energies of water and formamide on the Pt surface were calculated to be Ewat = 2.1 and Eform = 2.9 kcal/mole, respectively.
The properties of formamide-water/(TiO2, Pt) and ethanol-water/(TiO2, Pt) solutions were compared in similar environments. With the use of comparative analysis, the formamide-water interactions were correlated with the ethanol-water interactions on the same (anatase and platinum) surfaces. The activation energies of water and ethanol were calculated to be, respectively, Ewat = 3.5 and Eeth = 2.7 kcal/mole (on TiO2), and Ewat = 3.7 and Eeth = 2.9 kcal/mole (on Pt). It is easy to see that the ethanol and formamide activation energies are very close to each other. However, it should be stressed that only the water activation energies differ for these two different mixtures.
Water strongly influences the diffusion capabilities of formamide and ethanol on both TiO2 and Pt surfaces. At the same time, comparing the important radial distribution functions, we conclude that in the formamide-water/(TiO2, Pt) interactions water molecules actviley push formamide molecules from the surface to the bulk areas, while in the ethanol-water/(TiO2, Pt) interactions ethanol rather than water molecules dominate on the surface. Thus, including water in consideration, we see that it has a significant influence on the dynamic and structural behavior of both models (ethanol-water and formamide-water). We have found that it has different influence on the formamide/(TiO2, Pt) and ethanol/(TiO2, Pt) interaction processes, which results in different structural and diffusion effects. These effects determine the functional behavior of formamide and ethanol molecules since they are constituents of biological systems or agents in catalyzing the synthesis of biological molecules necessary for life.
SUPPLEMENTARY MATERIALS
Supplementary material is available on the publisher’s web site along with the published article Download Supplementary Material.
CONFLICT OF INTEREST
The author(s) confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
This work has been performed as part of a collaboration between JINR (Russia), RIKEN (Japan), and Keio University (Japan). The work has been supported in part by the Grant in Aid for the Global Center of Excellence Program to the Center for Education and Research of Symbiotic, Safe and Secure System Design from Japan's Ministry of Education, Culture, Sport, and Technology. The MD simulations have been performed using computer software, hardware facilities, and cluster machines at the CICC (JINR), RICC (RIKEN), and the Yasuoka Laboratory of Keio University (Japan). The authors would like to specially thank Mr. Sergei Negovelov (JINR) for technical assistance and helpful comments.
REFERENCES
[PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link]


