All published articles of this journal are available on ScienceDirect.
Regions which are Responsible for Swapping are also Responsible for Folding and Misfolding
Abstract
Domain swapping is a term used to describe a process when two or more protein chains exchange identical structural elements. Some cases of amyloid formation can be explained through a domain swapping mechanism therefore this deserves theoretical consideration and studying. It has been demonstrated that diverse proteins in sequence and structure are able to oligomerize via domain swapping. This allows us to suggest that the exchangeable regions are important in folding and misfolding processes of proteins, i.e. the residues from the swapping regions are typically incorporated into the native structure early during its formation. The modeling of folding of the proteins with swapped domains demonstrates that the regions exchanged in the oligomeric form in most cases are also responsible for folding and misfolding. For 11 out of 17 proteins, swapping regions intersect with the predicted amyloidogenic regions. Moreover, for 10 out of 17 proteins, high Φ-values (>0.5) belong to residues from the swapping regions. Our data confirm that the exchangeable regions are important in folding, misfolding, and domain swapping processes of the proteins, therefore the suggestion that domain swapping can serve as a mechanism for functional interconversion between monomers and oligomers is likely to be correct.
INTRODUCTION
Eisenberg and his colleagues [1, 2] have proposed a mechanism for protein oligomerization, 3D domain swapping. In a domain swapping oligomer, one segment of a monomeric protein is replaced by the same segment from another chain. Some cases of amyloid formation can be explained through a domain swapping mechanism where the swapped segment is either a beta-hairpin or another conformation. From the time of definition of domain swapping in diphtheria toxin [1], three-dimensional domain swapping has been observed in more than 40 different proteins, among them in such amyloidogenic proteins as prions [3, 4], beta2-microglobulin [5, 6], cystatins [7-11], and in such important proteins as p13suc1 [12-15], interferon [16, 17] and others. The understanding of oligomerization via domain swapping is important for theoretical and practical tasks because a swapping mechanism is critical for some protein functions [12-15].
For p13suc1 it has been demonstrated that domain swapping and aggregation correlate, which suggests that they share a common mechanism [14]. It has been established that p13suc1 from fission yeast belongs to the Cks protein family [18] and is required for the function of cyclin-dependent kinase (Cdk) proteins during cell cycle progression [19]. p13suc1 has two native states, a monomer and a domain-swapped dimmer, and the monomer-dimer equilibrium is controlled by two conserved prolines in the hinge loop. The X-ray crystal structure of p13suc1 at 1.95 Å resolution was reported [12] (see Fig. 1g and Table 2, row 17). The domainswapped part of suc1 is a single β-strand that cannot constitute an independently folded subdomain [12, 13]. To confirm this, the protein engineering analysis of the folding pathway of the monomer has been performed [13]. The experimental data on the transition state structure is expressed in Фf values [20]. Фf is close to 1 when a residue has its native conformation and environment in the transition state and to 0 when the residue is unfolded in this state. The exchanging strand in suc1, β4, forms critical contacts with the rest of the protein in the folding nucleus and the Φ-values for the hinge residues are between 0.5 and 0.8 [13]. Thus, folding and association should be tightly coupled, with pairing of β2 and β4 occurring early in the folding pathway of the dimer. So, it has been demonstrated for one protein that the exchangeable region is responsible for folding and misfolding.
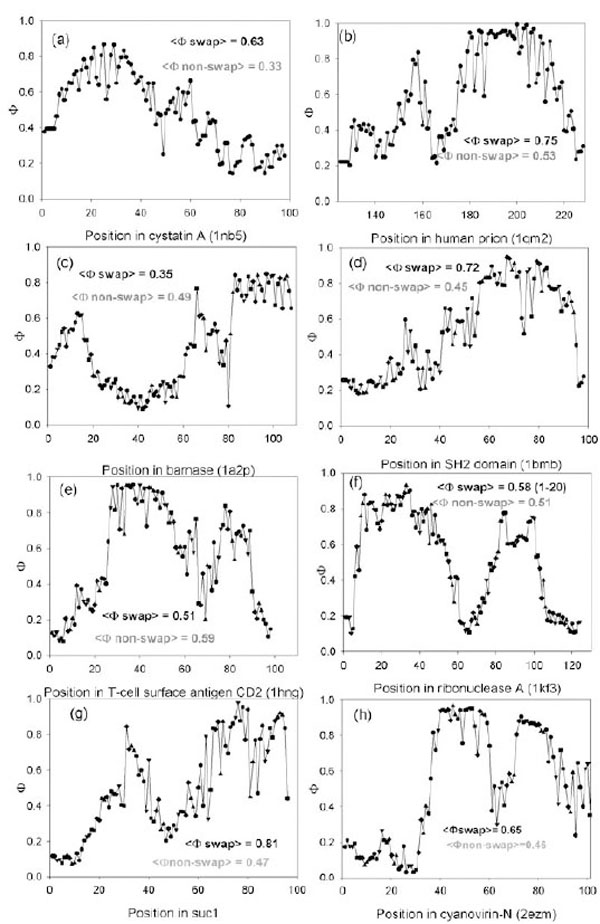
Predicted Ф-value profiles for weight investigated proteins. For each protein, the average Ф-value inside swapping and over non-swapping region is presented.
Prediction of Amyloidogenic Regions for Proteins with Swapping Domain
 |
Since polypeptide chains can fold into native structures or misfold into amyloid fibrils, there is a competition between the processes of folding and misfolding. A crucial event of protein folding is the formation of a folding nucleus, which is a structured part of the protein chain in the transition state. It has been demonstrated that there is a correlation between locations of residues involved in the folding nuclei and locations of predicted amyloidogenic regions [21, 22]. It has been demonstrated also that the average Φ-values are significantly greater inside amyloidogenic regions than outside them [21-23]. We have found that fibril formation and normal folding involve many of the same key residues, giving an opportunity to outline the folding initiation site in protein chains [21].
The goal of this work is to compare amino acid residues which are crucial for folding, misfolding, and swapping processes of the same proteins.
One can hypothesize that regions which are responsible for aggregation and protein folding will often appear as swapping regions in the proteins with swapped domains. For this purpose we collected 17 pairs with known 3D structures of swapped domains in the oligomeric form and 3D structures of the monomeric form. For these proteins, we calculated the amyloidogenic/aggregation regions using our program (FoldAmyloid/FoldUnfold) [24, 25] and for the monomeric form of proteins we calculated Φ-values for each residue also using our approach [26].
The modeling of folding of the protein with swapped domains demonstrates that in most cases the regions exchangeable in the oligomeric form are also responsible for folding and misfolding. After considering examples of 3D domain swapping it has been suggested that domain swapping can serve as one of the mechanisms for functional interconversion between monomers and oligomers and as one of the mechanisms for evolution of some oligomeric proteins [2].
MATHERIALS AND METHODOLOGY
Prediction of Amyloidogenic Regions in Proteins
For prediction of amyloidogenic regions, we used the previously described [24, 25, 27, 28] method of prediction of regions with a large number of contacts per residue in protein sequences. For each amino acid residue in the protein sequence, an expected number of contacts per residue are attributed according to the type of the residue (which is the average number of contacts at a distance below 8 Å for the given type of residues in 3D structures of proteins [27, 28]). Then, the values are averaged with a sliding window of seven (or five) residues [25]. In the obtained profile, the regions within which all residues have values above the threshold (21.4 expected contacts per residue) are predicted as amyloidogenic if the size of such a region is not smaller than the sliding window [25, 27, 28]. Thus, the predicted amyloidogenic regions are those which have a large number of expected contacts per residue.
We tried to predict amyloidogenic regions not only by our method but by other methods allowing (as stated by their authors) to predict amyloidogenic regions. But at first, we decided to test the quality of the predictions of these methods (as well as of our method) on the seven proteins for which amyloidogenic fragments are experimentally known. We used TANGO (dis.embl.de) and ZYGGREGATOR (http://www-vendruscolo.ch.cam.ac.uk/zyggregator.php). The predictions we made using all the three methods are shown in Table 1.
Comparison of Predictions of Amyloidogenic Regions by Different Methods
| Name of the protein | PDB entry | Experimentally investigated amyloidogenic regions | Regions predicted | ||
|---|---|---|---|---|---|
| by our method | by Tango | by Zyggregator | |||
|
|
|||||
| Acylphosphatase | 1aps | - | 19 - 20; | ||
| 16-31 [29]; | 19 – 25a; | 36 - 37 | |||
| 87-98 [29] | 91 - 98 | ||||
|
|
|||||
| β2-microglobulin | 1im9 | 20-41 [30]; | 24 - 30; | 61 - 69 | 24 - 26; |
| 59-71 [31]; | 60 - 70 | 63 - 66 | |||
| 83-89 [6] | |||||
|
|
|||||
| Gelsolin | 1kcq | 52-62 [32] | 1 - 7 | - | 30; |
| 32 -33; | |||||
| 40 - 41 | |||||
|
|
|||||
| Transthyretin | 1bm7 | 10-19 [33]; | 10 - 17; | 107 - 111 | 28; |
| 105-115 [34] | 28 - 34; | 93 - 94; | |||
| 105 - 113 | 117 - 118 | ||||
|
|
|||||
| Lysozyme | 193l | 49-64 [35] | - | 28; | 25 - 26; |
| 54 - 65; | 28 - 29; | ||||
| 106 - 113; | 31; | ||||
| 121 - 129 | 55 - 56 | ||||
|
|
|||||
| Myoglobin | 1wla | 7-18 [36]; | 8 - 14; | 66 - 72 | 10 - 12; |
| 101-118 [37] | 27 - 33; | 14; | |||
| 100 - 116; | 67 - 70; | ||||
| 134 - 140 | 104; | ||||
| 109 | |||||
|
|
|||||
| Human prion | 1qm0 | 169-213 [38] | 136 - 142; | - | 126 - 128; |
| 159 - 166; | 177 - 179; | ||||
| 176 - 183 | 190; | ||||
| 212 - 213; | |||||
| 215 | |||||
a Bold type is used for the predicted regions which intersect with the experimentally obtained data.
One can see that TANGO does not find the largest part of experimentally revealed amyloidogenic fragments (only two of 12 experimental amyloidogenic regions are correctly predicted, and one (for myoglobin) is in the wrong place). ZYGGREGATOR works better for this set of proteins (seven of 12 amyloidogenic regions are correctly predicted, that is, intersect with real amyloidogenic fragments) but ZYGGREGATOR predictions are still worse compared to our method (we predict correctly 10 of 12 experimentally revealed amyloidogenic fragments).
As both methods do not give good predictions of amyloidogenic regions for proteins for which the quality of predictions can be evaluated, we could not add predictions made by these methods to our manuscript.
Theoretical Search for Folding Nuclei
We model the process of reversible unfolding of the protein "normal" (native) globular structure into the unfolded state at the point of thermodynamic equilibrium (where the free energies of the folded and unfolded states are equal). Under these conditions, only the completely folded and completely unfolded states are observed while all other states (misfolded, partially folded etc.) are destabilized. The pathways of folding and unfolding coincide and all dead-ends are destabilized, so the protein chain behavior can be approximated as a reversible folding/unfolding process.
We start from a known tertiary structure of the investigated protein in the native state and stepwise unfold its amino acid residues. A link of five residues is unfolded in a single step (this link size was shown to be optimal for predictions of folding nuclei in globular proteins) [39]. Finally, we obtain a completely unfolded state. The unfolded residues lose all contacts that existing in the tertiary structure but gain the entropy of the coil (except for the entropy which is expended on fixation of unfolded loops that protrude from the folded part of the structure). Thus, any amino acid residue in our model can exist in one of the two states: folded, where it has all of its native contacts with the other folded residues, and unfolded, where it has no contacts but has higher entropy.
Considering all the ways of protein structure unfolding, we obtain a network of protein folding/unfolding pathways. The free energy of any state is calculated as follows:
where nI is the number of native atom-atom contacts in the native-like part of I (nI does not include contacts of neighbor residues, which also exist in the coil; in this work, we consider two atoms to form a contact if their centers are separated by less than 6Å, which is the optimal value of this parameter for folding nuclei predictions [39]); ε is the energy of one contact (all contacts are assumed to be equal in energy); ηI is the number of residues in the unfolded part of I; T is the temperature; σ is the entropy difference between the coil and the native state of a residue (we take σ =2.3R [40], where R is the gas constant). The sum Σ is taken for all closed unfolded loops that protrude from the native-like part of I. For the loop between fixed residues k and l, Sloop is calculated as follows [41]:
where rkl is the distance between the Cα atoms of residues k and l, a= 3.8Å is the distance between the neighbor Cα atoms in the chain, and A is the persistence length for a polypeptide (according to Flory [41], we take A = 20Å). The term (5/2 R ln|k ( l| is the most significant in this equation; the coefficient (5/2 (rather than Flory's value (3/2) follows from the condition that the loop cannot penetrate inside the globule [42].
Calculation of Φ-Values
Since in our model all native contacts have equal energy and non-native contacts are absent, the Φ-value is a fraction of native contacts formed in the transition state compared to the native state [39]:
where Δr(n0) is the number of contacts deleted by the mutation in the given amino acid residue r in the native state of the protein while <Δr(nI)>I# is the number of contacts deleted by the mutation averaged over all transition states found with our method. We consider all mutations on Gly; if a residue in the wild-type protein is already Gly, we take its probability to be structured in the transition state ensemble [26].
Creation of a Database of Swapped Proteins
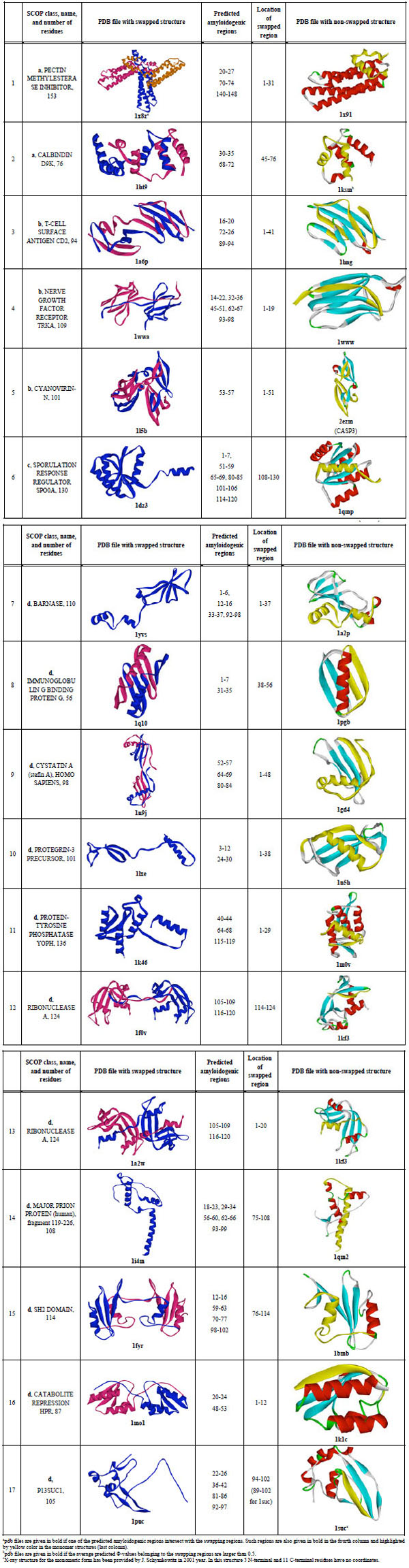
First, all entries where a word "swap" was met were selected from the PDB database. Then all these entries were manually processed and those where the word "swap" was not related to real swapping were excluded according to the SCOP [43]. Multi-domain proteins and proteins with split domains (consisting with non-continuous chains) according to the SCOP were excluded. Large proteins (larger than 200 amino acid residues) were also excluded. For each protein, a non-swapped 100% homolog has been found using BLAST [44]. If a swapped protein had no non-swapped 100% homolog, the protein was excluded. There are 16 pairs where we have PDB entries for swapped and non-swapped structures (see Table 2). Visual inspection of the spatial structures has been done to explain which region of non-swapped structure was swapped in the swapped structure. One additional pair for suc1 protein has been added because the X-ray structure for the monomeric form was provided by J. Schymkowitz in 2001 and later this protein was studied by us [36].
RESULTS AND DISCUSSION
Modeling of Folding of Proteins with Swapped Domains. Intersection of Experimentally Determined Swapping Regions with the Predicted Folding Nuclei
One can hypothesize that regions which are responsible for aggregation and protein folding will often appear as swapping regions in the proteins with swapped domains. For this purpose we collected 17 pairs with known 3D structures of swapped domains in the oligomeric form and 3D structures of the monomeric form.
Using a theoretical method, we searched for the position of the folding nuclei in the 3D structures of the monomeric form during their "normal" folding process from the unfolded state into their folded native structure. Using the method which (as we have previously shown earlier [26, 39, 45]) allows predicting the position of folding nuclei reasonably well (the correlation coefficient between predicted and experimentally known Φ-values reaches 65% if the native 3D structure used in the modeling is of high quality, see [39]), we modeled the behavior of each protein molecule at the point of thermodynamic equilibrium (i.e. under the conditions when unfolded and native states are equally stable and all the other states are unstable). The behavior of the protein molecule is modeled as a simplified sequential reversible unfolding of its known native 3D structure (see MATERIALS AND METHODOLOGY). The obtained network of folding/unfolding pathways is further analyzed by the dynamic programming method [46] to find transition states and (correspondingly) folding nuclei. The involvement of a residue in the folding nucleus (or rather, in the ensemble of the folding nuclei) is reflected in its Φ-value, which is unity when this residue has all of its native contacts in the transition state and zero when this residue has no contacts in the transition state.
We tested whether the theoretically found folding nuclei (Φ-values larger than 0.5) intersect with the experimentally found swapping regions. It appears that for 10 out of 17 proteins, high Φ-values (> 0.5) belong to residues from the swapping regions (such pdb files are given in the bold type, the last column in Table 2). The profiles of Φ-values for eight proteins are shown in Fig. (1). For cystatin A, the average predicted Φ-value inside swapping regions is higher (0.63) (see Fig. (1a)) than in the non-swapping one (0.33). The average predicted Φ-value for prion molecule inside swapping regions is higher (0.75) than in the non-swapping one (0.53). In Fig. (1b) one can see that the C-terminus of the prion molecule has higher Φ-values than the N-terminus. Moreover, the average predicted Φ-value inside amyloidogenic regions is higher (0.79) than in the non-amyloidogenic one (0.43) [23]. At the same time the average predicted Φ-value for a barnase molecule inside swapping regions (1-37) is lower (0.35) than in the non-swapping one (0.49), and in addition it is less than 0.5.
Thus, we demonstrate that theoretically found folding nuclei (Φ-values larger than 0.5) intersect with experimentally found swapping regions. This means that swapping regions are likely to be present in the folding nucleus of a protein when the protein folds into its native structure.
Intersection of Predicted Amyloidogenic Regions with Experimentally Determined Swapping Regions
Previously we have demonstrated that amyloidogenic regions are often predicted to be part of the folding nuclei in amyloidogenic proteins [21-23]. Therefore, we can hypothesize that amyloidogenic regions often play a crucial role not only in the amyloid fibril formation but also in the process of "normal" folding of amyloidogenic proteins into their native structure, since amyloidogenic regions compose part of the folding nucleus in these proteins. Inasmuch as some cases of amyloid formation can be explained through a domain swapping mechanism one can suggest that regions responsible for the amyloid formation will intersect with swapping regions.
Further, we have compared the predicted amyloidogenic regions for the 17 proteins where swapping regions have already been outlined experimentally. The prediction of amyloidogenic regions was made by the previously described [25, 27, 28] method (see also MATERIALS AND METHODOLOGY) which predicts amyloidogenic regions using only the amino acid sequence. For each amino acid residue, the method predicts the number of expected contacts and the regions within which all residues with a large number of expected contacts are predicted as amyloidogenic regions. As demonstrated previously [25], this method is able to predict amyloidogenic regions.
In Table 2, the predicted amyloidogenic regions for each of the 17 investigated proteins are shown. One can see that for 11 out of 17 proteins, swapping regions intersect with the predicted amyloidogenic regions (such pdb files are given in bold, third column). It should be noted that practically in all cases the swapping region is at the termini of the protein chain.
Thus, both comparisons (predicted folding nuclei vs. experimentally known swapping fragments and predicted amyloidogenic fragments vs. experimentally known folding nuclei) indicate that the location of swapping regions intersects with both the folding nuclei and the location of amyloidogenic regions. In other words, nucleation centers for folding and for misfolding and swapping regions often intersect.
Description of Globular Proteins Involved in Amyloidogenesis
Several important cases deserve a special consideration. It has been shown that such proteins as the cystatins and the prions can form dimers via a three-dimensional domain swapping mechanism which may be involved in amyloidogenesis as has been hypothesized [3, 4, 7-11].
Cystatins were the first amyloidogenic proteins which oligomerize through a 3D domain swapping mechanism [7]. It has been shown that oligomerization of human cystatin C leading to amyloid deposits in blood vessels is greatly accelerated with a naturally occurring Leu68Gln variant resulting in fatal amyloidosis in early adult life (Patients suffer such disease as Hereditary Cystatin C Amyloid Angiopathy which is a rare fatal amyloid disease) [10, 47]. It has been demonstrated that higher aggregates for cystatin C may arise through a domain-swapping mechanism when partially unfolded molecules are linked into multitude chains [9]. For cystatin A the N-terminal part of the molecule consisting of two beta-strands and one helix is exchanging under formation of domain swapping. It has been shown that the large conformational perturbation is needed for domain swapping [8]. It should be underlined here that the N-terminal part of the cystatin A has high predicted Φ-values. This confirms the hypothesis that regions which are important for folding are also important for swapping.
The crystal structure of human prion protein in a dimer form at 2 Å resolution has been described [3]. The dimer results from the three-dimensional swapping of C-terminal helix 3 and the rearrangement of the disulfide bond. An interchain two-stranded antiparallel beta-sheet is formed at the dimer interface by residues that are located in helix 2 in the monomeric NMR structures [3].
In the partially unstructured human prion protein, we predict an amyloidogenic region detected by experimentally (169-213 [38]). The first α-helix near the N-terminus appeared to have lower protection to solvent exchange compared to the other helices [48]. The N-terminus of the molecule appears to be predisposed to adopt multiple conformations that may feature in the transition from PrPC to the toxic PrPSc form [48]. It has been shown that this fast-folding protein has a transition state that is not compact (the m value analysis gives a βt value of only 0.3) but contains a developing nucleus between helices 2 and 3 [49]. This is in agreement with our prediction (see Fig. 1b) where residues corresponding to the second and third helices have high Φ-values. There are two residues with large Φ-values (V180 and M206), both of which are squarely on the interface between helix 2 and helix 3. These residues form the major part of the contact area in the central region of this interaction. The authors of the paper underline that if a mutation in the nucleus had a negligible effect on stability but still led to the formation of irregular conformations during folding then one should suggest an easily perturbed folding mechanism for such a protein [49]. It is notable that in inherited forms of human prion disease, where point mutations produce a lethal dominant condition, 20 of the 33 amino acid replacements occur in helices 2 and 3 (i.e. mutations map to the regions directly involved in helix swapping [49]). This crystal structure suggests that oligomerization through 3D domain-swapping may constitute an important step on the pathway of the PrP(C) --> PrP(Sc) conversion [3].
It should be mentioned here that the two proteins considered in this section are involved in the disease. For these proteins we observe intersection between regions important for folding and misfolding. This confirms our hypothesis that if the regions which are important for folding intersect with the regions which are responsible for amyloid formation, then such proteins can with higher probability misfold in appropriate environmental conditions to amyloid fibrils involved in vivo in various “amyloid” diseases.
By modeling the folding of 17 proteins with swapped domains we observe that regions, that are responsible for swapping, are also responsible for folding and misfolding.
ACKNOWLEDGEMENTS
The author is grateful to S. Garbuzinsky for the assistance in preparation of the dataset of proteins and to A.V. Glyakina for the assistance in preparation of some figures. This work was supported by the programs "Molecular and Cellular Biology" (01200959110) and “Fundamental Sciences to Medicine”, by the Russian Foundation for Basic Research (11-04-00763), and by a grant from the Federal Agency for Science and Innovations (#02.740.11.0295).
REFERENCES
[PubMed Link] [PMC Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PMC Link]
[PubMed Link] [PMC Link]
[PubMed Link]


