All published articles of this journal are available on ScienceDirect.
Multiple Unfolding Intermediates Obtained by Molecular Dynamic Simulations under Stretching for Immunoglobulin-Binding Domain of Protein G
Abstract
We have studied the mechanical properties of the immunoglobulin-binding domain of protein G at the atomic level under stretching at constant velocity using molecular dynamics simulations. We have found that the unfolding process can occur either in a single step or through intermediate states. Analysis of the trajectories from the molecular dynamic simulations showed that the mechanical unfolding of the immunoglobulin-binding domain of protein G is triggered by the separation of the terminal β-strands and the order in which the secondary-structure elements break is practically the same in two- and multi-state events and at the different extension velocities studied. It is seen from our analysis of 24 trajectories that the theoretical pathway of mechanical unfolding for the immunoglobulin-binding domain of protein G does not coincide with that proposed in denaturant studies in the absence of force.
INTRODUCTION
It has been shown by experiments that the immunoglobulin-binding domain of protein G (below, for short, protein G) has mechanical properties comparable with those of known elastomeric proteins [1, 2]. In addition to its mechanical stability, protein G shows such mechanical features as the fastest folding kinetics, small changes of mechanical and physical properties during long repeated stretching-relaxation cycles and ability to fold against residual forces. These features allow protein G to function in a challenging working environment requiring repeated stretching-relaxation [1, 2].
Protein G has topology in which there are hydrogen bonds between parallel N- and C-terminal β-strands. It has been shown that with this topology the N- and C-terminal β-hairpins hydrogen bonded with each other or via an additional β-strand, has most of the mechanically stable proteins [3-7].
The experimental studies of force unfolding of protein G have demonstrated that this protein unfolds by a two-state mechanism without an intermediate [8]. Protein G mechanically unfolds under the force of 180 pN at pulling velocity of 400 nm/s [3] and thermally unfolds at 89 ºC [9].
It was also shown that chemical denaturants have such an influence on the mechanical unfolding that the mechanical stability of protein G decreases systematically with an increase in denaturant concentration, which follows from the decreasing free energy barrier between the folded and transition states appearing at the protein unfolding. The decrease of the mechanical stability depends linearly on the increase of the denaturant concentration. However, upon mechanical unfolding, denaturants do not change the mechanical unfolding pathways and shift the position of the transition state. The mechanical unfolding pathway either considers or is a part of the chemical unfolding pathway. This conclusion was made from the coincidence of chemical and “mechanical” chevron plots [10].
A kinetic intermediate of protein G has been observed using a rapid mixer and fluorescence detection [11, 12]. The authors concluded that the kinetic intermediate for protein G was on the pathway [12], so the intermediate for protein L (the protein which has the similar three-dimensional structure but differs in the amino acid sequence) may be on the pathway as well [13].
The isolated fragment corresponding to the C-terminal β-hairpin of protein G which is included in the folding nucleus was studied in the experimental works [14, 15]. It was shown that the C-terminal β-hairpin of protein G is stable in water solution [14].
It is worth to underline here that Shimada and Shakhnovich demonstrated that protein G folds through multiple pathways, each of which passes through an on-pathway intermediate using the all-atom Monte-Carlo simulation with a Gō potential [16]. The authors observed three possible folding pathways for this protein. The first pathway (frequently observed) occurs due to the intermediate helix–N-hairpin, the second occurs due to the helix–C-hairpin, and the third takes place due to the formation of a β-sheet. The second and third pathways are observed more rarely than the first. Although all three pathways occur due to different intermediates, finally they are converged to the same key moment, i.e. the formation of a specific nucleus, which consists of amino acid residues from all three elements of secondary structure (helix and N- and C-hairpins).
Here, we study the mechanical properties of protein G at the atomic level upon stretching at a constant velocity using molecular dynamics simulations. The force-extension profiles of protein G have several force peaks, which indicates that several intermediate states appear in the mechanical unfolding trajectories. Analysis of the trajectories from molecular dynamic simulations showed that the mechanical unfolding of protein G is triggered by the separation of the terminal β-strands and the order in which the secondary-structure elements break is practically the same in two- and multi-state events and at different extension velocities studied: first the C-terminal β-hairpin is destroyed, then the α-helix, and the last the N-terminal β-hairpin. It is seen from our analysis of 24 trajectories that the theoretical pathway of mechanical unfolding for protein G does not coincide with that proposed in denaturant studies in the absence of force.
MATERIALS AND METHODOLOGY
Description of the Model and Method of Modeling
The object of the study was the immunoglobulin-binding domain of protein G (below, for short, protein G). Protein G (PDB entry 1pgb) consists of 56 amino acid residues and includes 853 atoms. This protein consists of two β-hairpins located at the termini (the N- and C-hairpins) and an α-helix between them (Fig. (1a)).
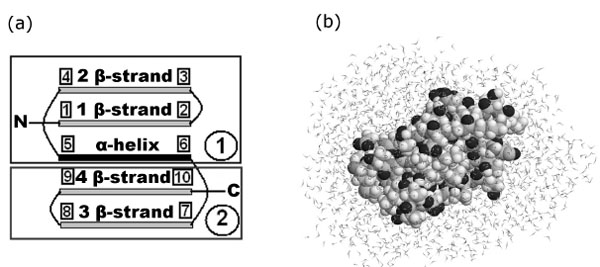
(a) Simplified representation of protein G. The first β-strand: 2Thr (19Cα) – 8Asn (133Cα), points 1-2; the second β-strand: 13Lys (209Cα) – 19Glu (295Cα), points 3-4; α-helix: 23Ala (348Cα) – 36Asp (549Cα), points 5-6; the third β-strand: 42Glu (617Cα) – 46Asp (691Cα), points 7-8; the fourth β-strand: 51Thr (761Cα) – 55Thr (825Cα), points 9-10. (b) Configuration of the system (protein G + water) after 50 ps relaxation.
The study has been carried out with the help of the method of molecular dynamics using the program PUMA, developed at the IMPB, RAS. The system of the classical motion equations of atoms has been resolved in the all-atom force field AMBER-99 [17].
A TIP3P model was used for water molecules, bonds and angles being not fixed, but set by appropriate potential functions. To maintain constant temperature, collisional thermostat was used [18,19]. The mean collision frequency of atoms with virtual particles was 10 ps-1, and the masses of virtual particles were 1 atomic mass unit. Equations of motion were integrated numerically by using the velocity version of Verlet algorithm [20] with a time step 1 fs (10-15 sec).
Initial coordinates of protein atoms were taken from the Protein Data Bank (PDB entry 1pgb). The protein was enclosed into a parallelepiped, filled with water molecules. The water molecules, which overlap with protein atoms, were removed. Thus, we received 1844 water molecules for protein G. The whole system (protein + water) was enclosed into a sufficiently large spherecylinder (diameter of spherecylinder is 60 Å and length is 280 Å) with impenetrable repulsive walls. This spherecylinder did not influence the dynamics of protein and water, and at the same time, did not allow water molecules go to the infinity, returned them into the modeling region. During the preparation of initial data for the first time, random velocities were assigned to all atoms and relaxation of the system was carried out with fixed terminal atoms (1N and 839Cα) of the protein G. A series of 24 such calculations in independent random collisional environments was made. Those systems relaxed during 50 ps served as initial systems for the following simulations (Fig. (1b)).
24 independent simulations, which differ in the initial data (coordinates and velocities) were carried out. Three extension velocity values were taken: v=0.125, v=0.0625 and v=0.005 Å·ps-1. Simulations were carried out at the temperature 350 K. Coordinates of all atoms of the protein were recorded every 5 ps.
The maximal length of trajectories was no more than 1200 ps under the extension velocity v=0.125 Å·ps-1 and 2400 ps under the extension velocity v=0.0625 Å·ps-1. By that time, in the protein there were no amino acid residues which had α-helical or β-structural conformations. Under the extension velocity v=0.005 Å·ps-1 the maximal length of trajectories was 7000 ps.
The number of contacts between elements of secondary structure and their changes during the force unfolding were analyzed. We calculated atom-atom and residue-residue contacts. Two residues have a contact if the nearest pair of their heavy atoms is at distance less than 5 Å. The calculation of the number of atom-atom contacts per residue in protein was carried out in the following way: two atoms were considered in contact with each other if their centers were at a distance of less than 5 Å. The atom-atom contacts between two adjacent residues as well as within one residue were not taken into account.
Accessible surface areas for each amino acid residue were analyzed. The secondary structure defined in sequential moments of times with the help of the program DSSP (Definition Secondary Structure of Proteins) [21].
Calculation of Folding Nuclei
To calculate Ф-values, structures which compose the ensemble of transition states, were selected from trajectories only under two extension velocities v=0.125 and 0.0625 Å·ps-1. From the trajectories received under extension of protein G with constant velocity, the structures which are situated in the region of the maximal force [22] and not lower than half of the force peak height were gathered. Since on some trajectories two and three force peaks were observed, structures corresponding to each force peaks were analyzed. The number of structures selected from the each force peak is shown in Table 1.
Average RMSD, Accessible Surface Area (ASA), and Fraction of Native Contacts in the Ensemble of Transition State Structures
| Number of Peak | v=0.125 Å·ps-1 | v=0.0625 Å·ps-1 | ||||||
|---|---|---|---|---|---|---|---|---|
| Number of Structures (Trajectories) | RMSD, Å | ASA, Å2 | Fraction of Native Contacts | Number of Structures (Trajectories) | RMSD, Å | ASA, Å2 | Fraction of Native Contacts | |
| First | 36 (3) |
9.50±0.02 | 3801±14 | 0.67 | 65 (4) |
9.47±0.03 | 3760±9 | 0.68 |
| Second | 38 (7) |
10.02±0.04 | 4133±16 | 0.50 | 38 (4) |
9.73±0.07 | 4161±13 | 0.47 |
| Third | - | - | - | - | 7 (2) |
11.14±0.09 | 4368±16 | 0.42 |
For every amino acid residue from the selected structures theoretical Ф-values were calculated as
(1)
where is the number of native atomic contacts which the amino acid residue has in transition state; is the number of contacts which the amino acid residue has in the native (initial) structure.
The calculated theoretical values may be compared with experimental values and their correlation may be obtained. Ф =1 indicates that both the residue structure and environment are native in the transition state. Ф =0 indicates that the residue in the transition state has no its own native structure or its native environment. Intermediate Ф-values are usually interpreted as evidence that the environment of the residue is native only partly [23-26]. Since, rarely occurring values have no structural interpretation [26], there is a low number of mutations for which experimental values are excluded from the comparison with theoretical calculations. Lists of the examined mutations for protein G is given in Table 2.
Experimental Ф-Values Obtained from the Unfolding of Protein G by Denaturant and Theoretical Ф-Values Calculated from the Modeling of Protein G Unfolding under the External Forces, Correlation Coefficients Between Theoretical and Experimental Ф-Values for the Ensemble of Transition State Structures for Protein G
| Mutation | Ф- values | |||||
|---|---|---|---|---|---|---|
| Experimental | Theoretical | |||||
| v=0.125 Å·ps-1 | v=0.0625 Å·ps-1 | |||||
| First Peak |
Second Peak |
First Peak |
Second Peak |
Third Peak |
||
| I6A | 0.38 | 0.61 | 0.22 | 0.63 | 0.22 | 0.22 |
| L7A | 0.32 | 0.55 | 0.3 | 0.55 | 0.34 | 0.23 |
| T11A | 0.02 | 0.21 | 0.02 | 0.23 | 0.02 | 0.1 |
| T16A | 0.00 | 0.69 | 0.58 | 0.71 | 0.56 | 0.53 |
| A20G | 0.02 | 0.58 | 0.41 | 0.59 | 0.33 | 0.26 |
| D22A | 0.23 | 0.84 | 0.73 | 0.84 | 0.68 | 0.39 |
| A26G | 0.31 | 1 | 0.61 | 0.77 | 0.51 | 0.3 |
| V29A | 0.26 | 0.64 | 0.64 | 0.68 | 0.46 | 0.34 |
| K31G | 0.23 | 0.64 | 0.39 | 0.64 | 0.37 | 0.16 |
| Q32G | 0.55 | 0.72 | 0.68 | 0.7 | 0.55 | 0.31 |
| Y33A | 0.20 | 0.69 | 0.58 | 0.68 | 0.49 | 0.41 |
| A34G | 0.21 | 0.67 | 0.55 | 0.66 | 0.51 | 0.27 |
| N35G | 0.19 | 0.75 | 0.65 | 0.74 | 0.63 | 0.27 |
| V39A | 0.16 | 0.52 | 0.33 | 0.54 | 0.3 | 0.22 |
| D46A | 0.96 | 0.8 | 0.82 | 0.84 | 0.79 | 0.84 |
| D47A | 0.67 | 0.77 | 0.73 | 0.65 | 0.68 | 0.74 |
| T49A | 0.84 | 0.79 | 0.8 | 0.83 | 0.79 | 0.82 |
| T51A | 0.44 | 0.75 | 0.35 | 0.75 | 0.31 | 0.33 |
| T53A | 0.27 | 0.57 | 0.33 | 0.59 | 0.33 | 0.34 |
| V54A | 0.16 | 0.59 | 0.28 | 0.59 | 0.27 | 0.16 |
| correlation coefficients | 0.48 | 0.57 | 0.53 | 0.62 | 0.76 | |
RESULTS AND DISCUSSION
Molecular Dynamics Simulations of Forced Unfolding of Protein G
To explore the mechanical resistances of protein G at the atomic level constant-velocity molecular dynamic simulations of the unfolding process were performed (24 simulations). Unfolding trajectories of protein G are shown in Figs. (2a), (3a) and (4a). Examination of the unfolding force-extension profiles shows that protein G unfolds through a relatively broad transition state ensembles and in most cases populates one or two intermediates (Figs. (2b,c), (3b,c,d) and (4b,c,d)).
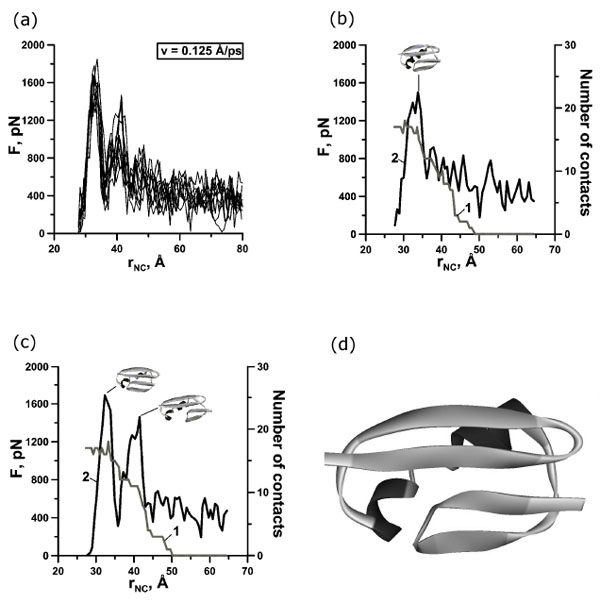
(a) Change of the reaction force F applied to termini of protein G in points of fixation, depending on distance rNC between them. There are 10 curves for extension velocity v=0.125 Å⋅ps-1. (b, c) Dependence of force (curve 2) and number of contacts between β-strands 1 and 4 (curve 1) on time for protein G for representative trajectories. Structures correspond to force peaks. (d) Structure of the first intermediate for representative trajectory.
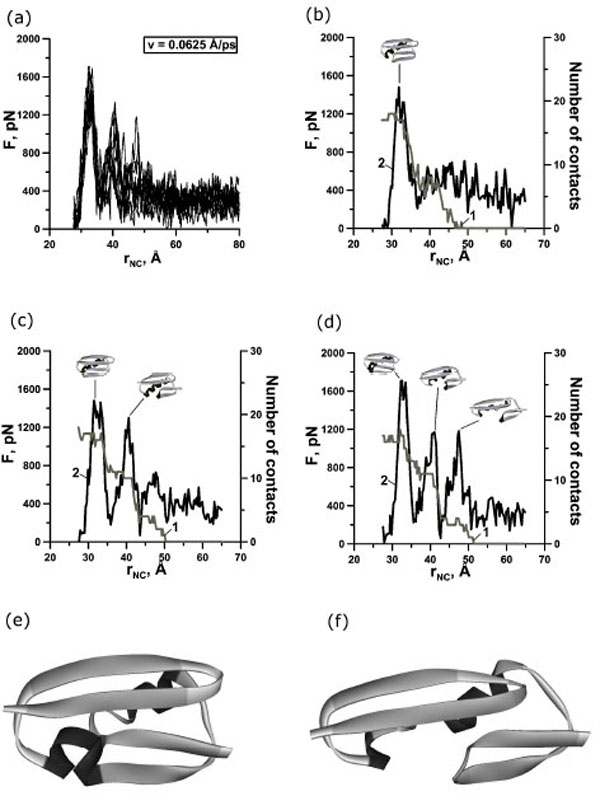
(a) Change of the reaction force F applied to terminuses of protein G in points of fixation, depending on distance rNC between them. There are 10 curves for extension velocity v=0.0625 Å⋅ps-1. (b, c, d) Dependence of force (curve 2) and number of contacts between β-strands 1 and 4 (curve 1) on time for protein G for representative trajectories with two-state (b), three-state (c) and four-state events (d). Structures correspond to force peaks. Structures of the first (e) and second (f) intermediates for representative trajectories.
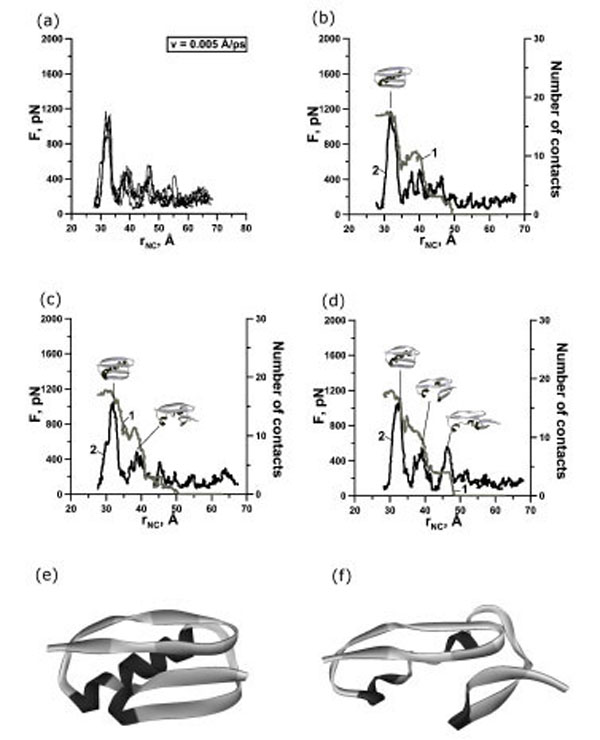
(a) Change of the reaction force F applied to terminuses of protein G in points of fixation, depending on distance rNC between them. There are 4 curves for extension velocity v=0.005 Å⋅ps-1. (b, c, d) Dependence of force (curve 2) and number of contacts between β-strands 1 and 4 (curve 1) on time for protein G for representative trajectories with two-state (b), three-state (c) and four-state events (d). Structures correspond to force peaks. Structures of the first (e) and second (f) intermediates for representative trajectories.
The maximal forces which arise during the simulations and the distance between the N- and C-termini for protein G which corresponds to the force were averaged for each velocity. The results are presented in Table 3. There is a tendency to lowering the force barrier due to the decreasing extension velocity. It is should be underlined here that the faster the pulling speed, the larger the force peak measured since the protein has less time to be thermally activated over the unfolding barrier [27]. Unfolding occurs after an extension of 5.5, 5.0 and 4.5 Å for three velocities (0.125, 0.0625 and 0.005 Å·ps-1) and involves the break of contacts between the N- and C-terminal β-strands.
Average Maximal Force <Fmax> and Average Increasing of Distance < - > Between the N- and C- Termini for Protein G under Extension Velocities 0.125, 0.0625 and 0.005 Å·ps-1
| Extension Velocity | Number of Peak (and Trajectories) | <Fmax>, pN | < >,Å | < - >,Å |
|---|---|---|---|---|
| v=0.125 Å·ps-1 | First (10) |
1647±37 |
33.2±0.3 |
5.5±0.3 |
| Second (7) |
1230±78 |
40.5±0.7 |
12.8±0.7 |
|
| Third (0) |
- |
- |
- |
|
| v=0.0625 Å·ps-1 | First (10) |
1503±36 |
32.6±0.4 |
5.0±0.4 |
| Second (6) |
1144±59 |
40.8±0.4 |
13.1±0.4 |
|
| Third (2) |
1096±88 |
47.8±0.3 |
20.1±0.3 |
|
| v=0.005 Å·ps-1 | First (4) |
1302±17 |
32.2±0.4 |
4.5±0.4 |
| Second (3) |
697±39 |
41.8±2.7 |
14.1±2.7 |
|
| Third (1) |
763 |
46.5 |
18.8 |
is the initial distance between N- and C- termini.
is the distance between N- and C- termini at the time when the force is maximal.
In our case we observed one, two, and three force peaks on the different trajectories (Figs. 2,3,4 and Table 1). Two force peaks on the trajectories appear in most cases for protein G (see Table 1). These force peaks appear during the first 150 ps of unfolding under the extension velocity v=0.125 Å·ps-1 and 400 ps under the extension velocity v=0.0625 Å·ps-1. There aren’t trajectories with three force peaks under the extension velocity v=0.125 Å·ps-1. Analysis of structures showed that about 50% and 35% of native contacts remains in the first and in the second intermediates (Figs. (2d), (3e,f) and (4e,f)), correspondingly.
Analysis of the dependences of the force and the number of contacts between β-strands 1 and 4 on the stretching time revealed that for protein G the first, second and third force peaks are correlated with a dramatically decreasing the number of contacts between β-strands 1 and 4 for all trajectories (Fig. (2b,c) and Fig. (3b,c,d)). Moreover, the order of disappearance of contacts between β-strands is the same for 20 trajectories under extension velocities 0.125 and 0.0625 Å·ps-1: the first between β-strands 1 and 4, then between β-strands 3 and 4 (the C-terminal β-hairpin), and finally between β-strands 1 and 2 (the N-terminal β-hairpin) (Fig. (5a,b)).
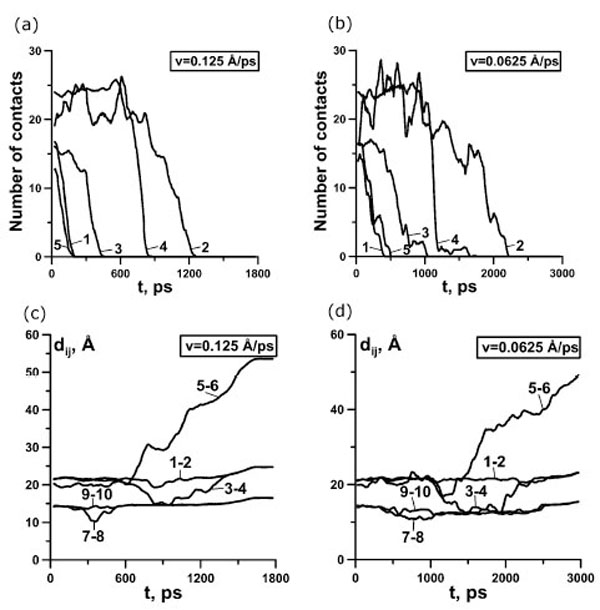
(a, b) Dependence of the number of contacts on time for protein G for representative trajectory. 1, contacts between β-strands 1 and 4; 2, contacts between β-strands 1 and 2; 3, contacts between β-strands 3 and 4; 4, contacts between N-hairpin and α-helix; 5, contacts between C-hairpin and α-helix. (c, d) Dependence of distances between the ends of different elements of secondary structure on time for representative trajectory. 1-2 distance between the ends of the first β-strand, 3-4 – the second β-strand, 5-6 – α-helix, 7-8 – the third β-strand, 9-10 – the fourth β-strand. (a, c) 0.125 Å⋅ps-1, (b, d) 0.0625 Å⋅ps-1.
The study of the distances between the ends of the elements of secondary structure demonstrates that, in all cases, β-strands 1 and 4 are only slightly stretched (curves 1-2 and 9-10 Fig. (5c,d)), and β-strands 2 and 3 are bent (curves 3-4 and 7-8 Fig. (5c,d)). The bends (Fig. (5c,5d)) of β-strands 2 and 3 correlates with the decreasing the number of contacts (Fig. (5a,b)) between β-strands, which composed the N- and the C-terminal β-hairpins, correspondingly.
Fig. (6) demonstrates the fractions of time of existence of native contacts between elements of secondary structure for all trajectories under the extension velocities 0.125 Å·ps-1 (Fig. (6a)) and 0.0625 Å·ps-1 (Fig. (6b)). From these data we also see that in most cases at first contacts between the N- and C-hairpins disappear, then between the C-hairpin and α-helix, and at last between the N-hairpin and α-helix. It should be underlined here, that the order of unfolding of the elements of secondary structure correlates with the presence of a number of atom-atom and residue-residue contacts in the initial structures: β-strands 1 and 4 (759 atom-atom and 16 residue-residue contacts), β-strands 3 and 4, the C-terminal β-hairpin (662 atom-atom and 16 residue-residue contacts), and finally between β-strands 1 and 2, the N-terminal β-hairpin (887 atom-atom and 24 residue-residue contacts). From the analysis of protein structures, we can suppose that the more contacts between the elements of secondary structure, the more mechanically stable the element. There are more atom-atom contacts between β-strands 1 and 4 than between β-strands 3 and 4, but contacts between β-strands 1 and 4 disappear earlier than those between β-strands 3 and 4. This occurs because the topology of protein G and direction of extensional force are such that until there are contacts between β-strands 1 and 4 the C-terminal β-hairpin can not be destroyed. And only after disappearance of contacts between β-strands 1 and 4, first there takes place unfolding of the C-terminal β-hairpin (662 contacts) and then the N-terminal β-hairpin (887 contacts).
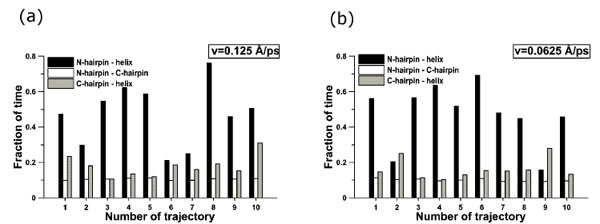
Fraction of time of existence of native contacts between elements of secondary structure: (a) 0.125 Å⋅ps-1, (b) 0.0625 Å⋅ps-1.
In addition to the analysis of the order of disappearance of contacts between elements of secondary structure, we also studied the order of destruction of secondary structure elements. Fig. (1) and Fig. (7) in Supplementary materials show representative mechanical unfolding trajectories for protein G. A complete analysis revealed that, in protein G, in most of cases, the order in which the secondary structure elements break is practically the same: first the C-terminal β-hairpin is destroyed, then the α-helix, and the last the N-terminal β-hairpin. The order does not depend on the extension velocities.
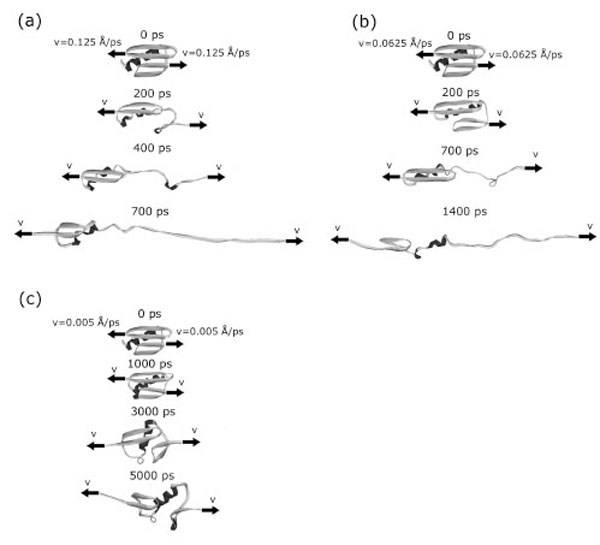
The mechanical unfolding of protein G occurs through at least two pathways. At first pathway (in 17 cases from 24) two intermediate structural blocks [the N-terminal β-hairpin +α-helix] and [the С -terminal β -hairpin] appeared (Fig. (1a)). So, at the initial event the force is loaded onto the C-terminal β-hairpin detaches it from the first cluster and destroys. Then the force is loaded onto the α-helix and stretches it. And finally, the force is loaded onto the N-terminal β-hairpin and destroys it. In six cases (the second pathway) the N- and C- terminal β-hairpins separate from each other and from the α-helix. And first the C-hairpin, then the α-helix, and then the N-hairpin are destroyed. And in one case under the extension velocity v=0.005 Å·ps-1 we observed a quite different unfolding pathway. At this pathway two intermediate structural blocks also appeared. But these structural blocks are [the N-terminal β-hairpin] and [the С-terminal β-hairpin+α-helix] (Fig. (7c)).
Calculation of Ф-Values upon Force Unfolding and Their Comparison with Those Previously Reported in Conventional Ф-Value Analysis
To compare the experimental Ф-values reported in the literature obtained by conventional analysis (in the absence of force) and Ф-values obtained by us upon modeling of mechanical unfolding of protein G under stretching at constant velocity using molecular dynamics simulations it is necessary to identify an ensemble of structures that represent the transition states. This ensemble must include structures that immediately precede rapid protein unfolding.
In steered molecular dynamics when we have several force peaks, the first barrier corresponds to the peak in the applied force at the transition from the native to intermediate I1 state, the second force peak corresponds to the transition from I1 to I2, and the third force peak corresponds to the intermediate I2 unfolding. Therefore, we collected the ensembles of transition states for each peak and separately calculated Ф-values for each ensemble of transition states (see Table 2).
Some characteristics of the ensembles of transition states are represented in Table 1. One can see that the average RMSD and the accessible surface area increase with the number of peaks. RMSD for v=0.125 Å·ps-1 in all cases is higher than for v=0.0625 Å·ps-1. The fraction of native contacts in the transition state structures is also represented in Table 1.
The Ф-values for the forced unfolding are significantly higher than those observed in the absence of force, especially in the region of N-terminal β-hairpin (Fig. 8 and Table 2). This would indicate that the ensemble of transition states for forced unfolding is more structured than the ensemble of the transition states in the absence of force. From Table 2 one can see that the correlation coefficient between experimental Ф-values and theoretical Ф-values obtained from the mechanical unfolding depend on the number of peaks and the extension velocity values and changes from 0.48 to 0.76. Correlation coefficient increases with increasing number of peaks and decreasing extension velocity. Correlation coefficients between theoretical and experimental Ф-values, averaged by the amino acid residues included in elements of secondary structure is 0.58 if to consider the region of the first force peak for both extensional velocities (Fig. (8c,d)).
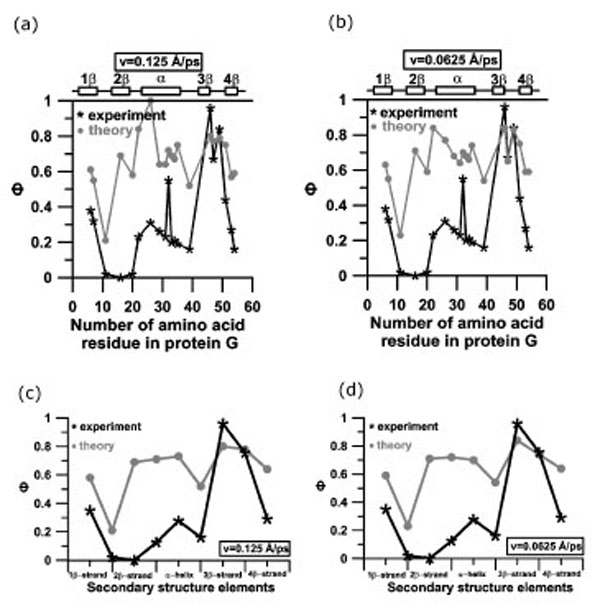
Profiles of experimental and theoretical Ф-values for protein G (a, b) and profiles of experimental and theoretical Ф-values for protein G, averaged over amino acid residues, included into elements of secondary structure (c, d): (a, c) v=0.125 Å⋅ps-1; (b, d) v=0.0625 Å⋅ps-1. Structures in transition states for calculation of Ф-values were taken from the region of the first force peak.
Studying the mechanical stability of a protein provides valuable information about the energy landscape underlying the folding/unfolding processes. A comparison of the results of calculation with the experimental data shows that the unfolding pathways for mechanical and chemical unfolding for protein G are very different. Analysis of the trajectories from molecular dynamic simulation showed that the mechanical unfolding of protein G is triggered by the separation of the terminal β-strands (strands β1 and β4). The interaction between these β-strands and the other secondary structure of the protein makes a fundamental stabilizing contribution in the presence of a stretching force. A similar situation is observed in our simulations for protein L (the protein which has the same three-dimensional structure but differ in amino acid sequence, paper in preparation) and in the work [28]: at first the contacts between the terminal β-strands break, and only then there is mechanical unfolding of the rest of the protein.
Examination of the unfolding force-extension profiles shows that the unfolding process for protein G can occur either in a single step or through intermediate states. A similar situation is observed in our simulations for protein L (paper in preparation). It has been demonstrated that mechanical unfolding process of ubiquitin, which has identical topologies with proteins L and G (ubiquitin-like fold), can occur either in a single step or through intermediate states [29]. Kinetics studies of other two-state proteins [30,31] suggest the presence of short lived intermediates that cannot be directly detected experimentally.
SUPPLEMENTARY MATERIAL
Supplementary material is available on the publisher’s web site along with the published article. Download Supplementary Material.
ACKNOWLEDGEMENTS
This work was supported by the Russian Academy of Sciences (“Molecular and Cell Biology” and “Fundamental Science – Medicine” programs), by the Russian Foundation for Basic Research (grants № 06-03-32814 and № 08-04-00561), by the “Russian Science Support Foundation” and by Howard Hughes Medical Institute (grant 55005607). Calculations were done at the Joint Supercomputing Center of the Russian Academy of Sciences.
REFERENCES
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]
[PubMed Link]
[PubMed Link] [PMC Link]
[PubMed Link] [PMC Link]
[PubMed Link]
[PubMed Link]


